![]()
Nous allons voir sur cette page comment réaliser la simulation de la planche de Galton en Python, au programme de Terminale Mathématiques.
Simulation de la planche de Galton en Python: introduction
Cette vidéo illustre le principe de cette planche : on laisse tomber une bille tout en haut du « système » (pyramide de clous). À chaque clou que rencontre cette bille, elle a le choix entre aller à droite ou à gauche.
On répète ceci avec un grand nombre de billes et tout en bas, on les récolte en observant leur distribution (la façon dont elles sont tombées).
Il s’avère qu’au final, toutes les billes forme une « courbe en cloche » appelée « courbe de Gauss » (je vais vite car le but de cette page n’est pas tant d’expliquer ce qu’est l’expérience que de la réaliser en Python). Pour plus d’informations, regarder la page de wikipedia.
Simulation de la planche de Galton en Python: le programme
from random import choice
c = 7
base = c * [0]
for bille in range(1000):
position = c // 2
for clou in range(c-1):
position += choice([-1,1])/2
base[ int(position) ] += 1
print( base )
Le programme n’est pas si long que ça au final… Expliquons-le !
Tout d’abord, j’importe la fonction choice du module random. Nous allons voir plus loin pourquoi elle est intéressante…
Je fixe le nombre de colonnes finales à 7 (c = 7). Les colonnes sont les endroits qui reçoivent les billes au final. Il faut que ce soit un nombre impair.
Ensuite, je définis une liste nommée base qui vaut initialement [0,0,0,0,0,0,0] (c éléments nuls). Les éléments de cette liste représenteront le nombre de billes qu’il y aura à la fin dans chacune des colonnes.
En ligne 6, j’initialise une boucle itérative pour simuler 1000 lâchers de billes.
Pour chaque simulation de lâchers, je fixe la position de départ de la bille: au milieu (donc c//2).
Ensuite, je pars du principe qu’il y a c – 1 lignes de clous (ce qui est toujours le cas), donc je simule la rencontre de c – 1 clous. Pour chacun d’eux, je choisis au hasard une direction. Ici, j’utilise choice([-1,1]) pour choisir entre « -1 » et « 1 ». Si « -1 » est obtenu, la position actuelle est diminuée de 0,5; sinon, elle est augmentée de 0,5.
À l’issue de la boucle itérative sur « clou », j’obtiens la position de la bille (entre 0 et c-1). Je n’ai plus alors qu’à incrémenter la valeur déjà contenue dans la liste base pour cette position (ligne 11 et 12).
Simulation de la planche de Galton en Python: résultats
Je vais effectuer 20 simulations de 1000 lâchers de billes :
from random import choice
c = 7
for n in range(20):
base = c * [0]
for bille in range(1000):
position = c // 2
for clou in range(c-1):
position += choice([-1,1])/2
base[ int(position) ] += 1
print( base )
J’obtiens :
[17, 83, 232, 316, 242, 97, 13] [18, 96, 232, 334, 221, 82, 17] [17, 85, 243, 304, 240, 98, 13] [10, 90, 217, 320, 246, 106, 11] [12, 88, 230, 319, 262, 75, 14] [13, 84, 245, 302, 245, 100, 11] [18, 94, 224, 332, 219, 101, 12] [16, 101, 241, 285, 254, 88, 15] [23, 92, 239, 302, 220, 103, 21] [21, 100, 218, 311, 224, 100, 26] [15, 113, 230, 288, 249, 89, 16] [15, 92, 231, 310, 252, 85, 15] [19, 100, 211, 308, 253, 86, 23] [12, 83, 237, 310, 248, 93, 17] [16, 97, 239, 302, 228, 103, 15] [20, 96, 210, 322, 236, 96, 20] [17, 97, 223, 313, 241, 97, 12] [14, 89, 246, 330, 216, 91, 14] [17, 87, 222, 333, 239, 86, 16] [15, 90, 246, 307, 222, 102, 18]
Représentation graphique
On va d’abord représenter en mode texte la liste obtenue avec une simulation. Bien entendu, je ne vais pas simuler le lâcher de 1000 billes (car je risque de manquer de place… comme disait Fermat !).
from random import choice
def simulation_galton(c = 7 , n = 20):
base = c * [0]
for bille in range(n):
position = c // 2
for clou in range(c-1):
position += choice([-1,1])/2
base[ int(position) ] += 1
return base
def graphique( L ):
M = max(L)
for l in range( max(L) ):
ligne = ''
for e in L:
if e == M:
ligne += ' * '
L[L.index(e)] -= 1
else:
ligne += ' ' * 3
print(ligne)
M -= 1
graphique( simulation_galton(n=50) )
qui donne par exemple :

Si l’on souhaite une représentation plus élégante, on pourra par exemple ajouter la fonction Python suivante :
def graph_plot( L ):
from numpy import arange
from matplotlib.pyplot import bar, show
c = len( L )
x = arange(0,c,1)
bar(x,L,width=0.8,color='red',alpha=0.5)
show()
qui donne, en lançant :
graph_plot( simulation_galton(n=1000) )
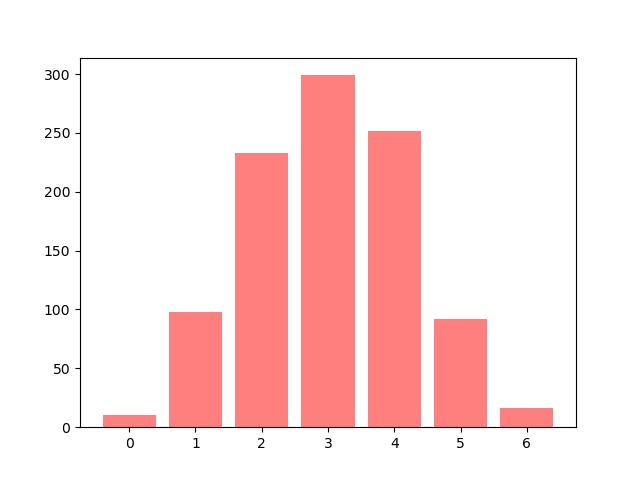
Bien sûr, cette dernière solution est meilleure car s’adaptant à de grandes valeurs de c et n.
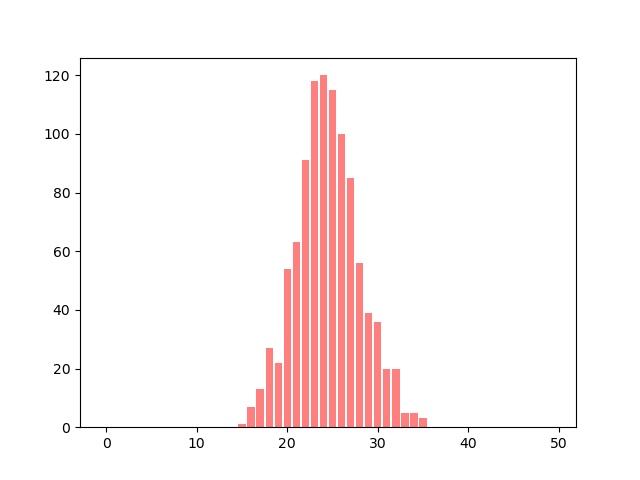
graph_plot( simulation_galton(c = 50, n=1000) )






merci beaucoup. Je peux avoir le fichier pithon à cette adresse (adresse supprimée) svp
Il suffit de copier le code. Je ne comprends pas votre demande.