Nous allons voir comment écrire des fonctions de tri en Python.
Tri en Python: avant-propos
Les histoires de tris en Python sont d’un importance capitale. En effet, si l’on souhaite trier une collection colossale, nous n’avons pas le droit d’utiliser un algorithme lent, un algorithme dit « naïf ». Pourquoi ?
La raison est simple: plus ce qu’il y a à trier est grand, plus ça va prendre de temps… et des ressources matérielles que nous n’avons pas toujours.
D’où la question de trouver un algorithme efficace…
Un tri naïf en Python
Le tri naïf consiste à parcourir la liste à trier et construire une autre liste créée à partir de la première en y insérant chaque élément convenablement.
Un premier tri naïf
def insertNaif(A,e):
if e < A[0] :
return [e] + A
else:
for n in range( 1 , len(A) ):
if e > A[n-1] and e <= A[n]:
return A[:n] + [e] + A[n:]
return A + [e]
def triNaif(L):
R = [ L[0] ]
for n in range(1,len(L)):
R = insertNaif(R,L[n])
return R
Un deuxième tri naïf
def triNaif(L):
R = []
while len(L) > 0:
m = L[0]
for i in range(1,len(L)):
if L[i] < m:
m = L[i]
R += [ m ]
L.pop( L.index(m) )
return R
Tri à bulles
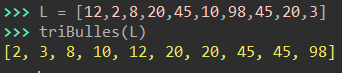
Sans doute le plus naïf des algorithmes, et donc le plus « gourmand » (en mémoire et en temps): il consiste à parcourir la liste à rebours en partant de sa fin, et de comparer chaque élément consécutif en partant du début jusqu’à l’élément courant. Si deux éléments ne sont pas dans l’ordre croissant, ils sont permutés.
Bien entendu, il faut absolument éviter les tris naïfs car leur complexité est quadratique.
def triBulles(L):
for i in range(len(L),0,-1):
for j in range(0,i-1):
if L[j+1] < L[j]:
L[j+1] , L[j] = L[j] , L[j+1]
return L
La version récursive:
def triPlace(L):
for n in range( 1 , len(L) ):
if L[n] < L[n-1]:
L[n-1] , L[n] = L[n] , L[n-1]
return triPlace( L )
return L
Une variante est d’insérer un booléen pour rompre la boucle principale.
def triBulles(L):
for i in range(len(L),0,-1):
liste_triée = True
for j in range(0,i-1):
if L[j+1] < L[j]:
L[j+1] , L[j] = L[j] , L[j+1]
liste_triée = False
if liste_triée == True:
break
return L
Le tri fusion en Python
Sur la page https://fr.wikipedia.org/wiki/Tri_fusion#Algorithme, on peut y voir un algorithme de tri fusion. Il consiste à fusionner deux listes en triant leurs éléments afin de donner une liste ordonnée.
Cet algorithme donne en Python:
def triFusion(L):
if len(L) == 1:
return L
else:
return fusion( triFusion(L[:len(L)//2]) , triFusion(L[len(L)//2:]) )
def fusion(A,B):
if len(A) == 0:
return B
elif len(B) == 0:
return A
elif A[0] <= B[0]:
return [A[0]] + fusion( A[1:] , B )
else:
return [B[0]] + fusion( A , B[1:] )
>>> L = [2,55,12,10,23,87,11,74,36,42,58]
>>> triFusion(L)
[2, 10, 11, 12, 23, 36, 42, 55, 58, 74, 87]Cet algorithme fait partie des algorithmes récursifs utilisant le paradigme du « diviser pour régner« .
