Complexité algorithmique - Mathweb.fr - Exemples concrets en Python

La complexité algorithmique d’un programme informatique est d’une importance majeure. En effet, c’est elle qui permet de vérifier l’efficacité de ce dernier.

Vous l’aurez donc compris, la complexité algorithmique est une grandeur : cela peut être un nombre, mais c’est très souvent un ordre de grandeur.

Un exemple élémentaire

Considérons le programme élémentaire suivant:

a, b = 3, 6
c = a + b
print(c)

La ligne 1 comporte 2 affectations; la ligne c comporte 1 affectation et une opération élémentaire (l’addition); la ligne 3 de comporte aucune affectation ni opération élémentaire.

On dit alors ici que la complexité (le coût) du programme est égal à 4. La complexité est constante.

Complexité algorithmique d’un programme avec une boucle

Penchons-nous maintenant sur le programme suivant:

def fct(n):
    s = 0
    for i in range(1,n+1):
        s += i
        
    return s

print( fct(10) )

Quelle est la complexité de la fonction fct(n) ? On voit qu’il y a une première affectation (s = 0). Ensuite, il y a n affectations pour la variable i ainsi que n opérations (s + i) et n autres affectations (pour s). Ainsi, au total, il y a 3n+1 opérations élémentaires, qui correspond à la complexité de la fonction. On dit ici que la complexité est linéaire car C(n) = 3n + 1, fonction donnant la complexité, est une fonction linéaire. On dit alors que la complexité est en $\mathcal{O}(n)$ : cela signifie qu’elle est quasi-proportionnelle à n.

Complexité algorithmique pour une boucle dans une boucle

def fctB(n):
    s = 0
    for i in range(1,n+1):
        s += i
        
    return s

def fctA(n):
    P = 1
    for j in range(1,n+1):
        P *= fctB(j)
        
    return P

print( fctA(10) )

Quelle est la complexité de la fonction fctA(n) ? On voit qu’il y a 1 première affectation (P = 1) puis, pour chaque valeur de j, il y a 1 affectation (pour la variable j elle-même), suivie de 3j + 1 pour le calcul de fctB(j), 1 autre opération (le produit de P par fctB(j)) et enfin 1 affectation pour P. Donc, pour être plus clair:

1 affectation avant la boucle;
pour j = 1, il y a 1 (j) + [3$\times$1+1] (fctB(1)) + 2 opérations élémentaires;
pour j = 2, il y a 1 (j) + [3$\times$2+1] (fctB(2)) + 2 opérations élémentaires;
pour j = 3, il y a 1 (j) + [3$\times$3+1] (fctB(3)) + 2 opérations élémentaires;
etc.
pour j = n, il y a 1 (j) + [3$\times$n+1] (fctB(n)) + 2 opérations élémentaires.

La complexité totale est donc:$$\begin{align}&n\times1 + 3(1+2+3+\cdots+n)+n\times1+2\times n \\=&4n+3\times\frac{n(n+1)}{2}\\=&\frac{3}{2}n^2+\frac{11}{2}n\end {align}$$C’est une complexité polynomiale de degré 2. On dit qu’elle est quadratique, et on dit qu’elle est en $\mathcal{O}(n^2)$.

Complexité algorithmique et recherche dichotomique

Supposons connue une liste ordonnée de n éléments. Nous souhaitons rechercher de manière dichotomique si un élément donné se trouve dans cette liste. On peut alors imaginer le programme récursif suivant:

def recherche_dichotomique(liste , element):
    n = len(liste)
    if len(liste) == 1:
        if liste[0] == element:
            return True
        else:
            return False
    elif liste[ n//2 ] == element:
        return True
    elif element > liste[n // 2]:
        return recherche_dichotomique( liste[n//2:] , element)
    else:
        return recherche_dichotomique( liste[:n//2] , element)
        
print( recherche_dichotomique([1,1,1,2,2,3,3,4,5,5,6,6,7,8,8,8,10] , 9 ) )

Je n’ai pas insisté sur le fait de trier à chaque fois la liste, car cela rajouterait un niveau de plus à la complexité, l’idée de cette page étant ailleurs.

Pour ce type de programme, nous n’allons pas nous lancer dans le calcul exact du nombre d’opérations élémentaires car c’est tout simplement impossible car ce nombre dépend de l’issue. En effet, le nombre peut être trouvé dès le début comme ne pas être trouvé du tout. Dans ce genre de situation, on préfère regarder le nombre maximum d’opérations.

Notons alors k ce nombre maximum. Alors, au maximum, la liste sera divisée k fois par deux et la taille de la “dernière liste” (à 1 élément) sera la partie entière de $\displaystyle\frac{n}{2^k}$. Ainsi,$$1 \leqslant \frac{n}{2^k}$$c’est-à-dire:$$2^k \leqslant n$$soit:$$k \leqslant \log_2(n).$$On dit alors que la complexité est logarithmique.

Les classes de complexité

Nous avons vu à travers ces quelques exemples qu’il pouvait exister plusieurs types de complexités. On appelle ces types des classes de complexité. Ces classes peuvent être vues ainsi:

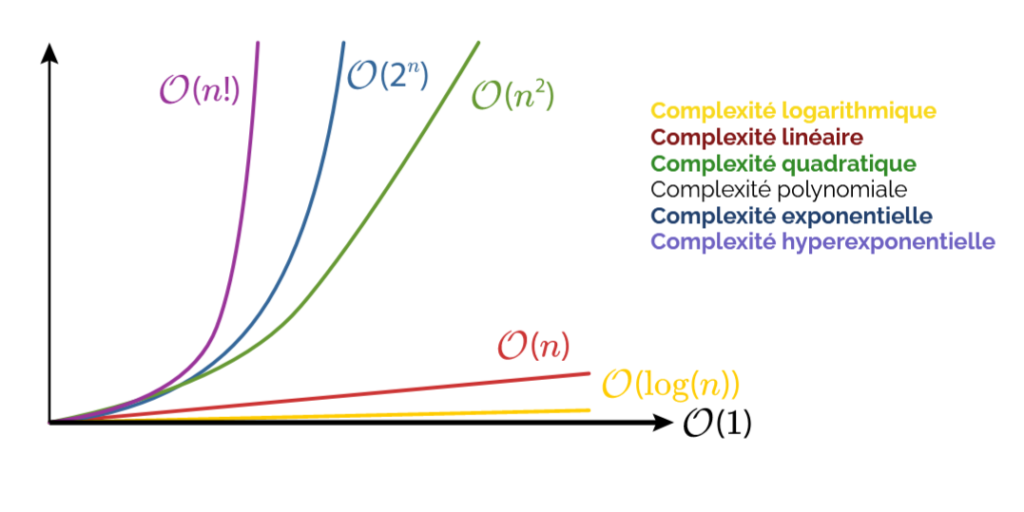
Source: https://view.genial.ly/5e8ed71d186d4e0dec349ef2/presentation-la-complexite-des-algorithmes

Il est donc important de connaître la classe de complexité d’un algorithme, d’un programme, pour savoir s’il est performant: en effet, plus sa classe se rapprochera de $\mathcal{O}(1)$ ou (\mathcal{O}(\log(n))) et mieux se sera. Mais il faut aussi avoir à l’esprit que certains problèmes n’ont toujours pas de solutions algorithmiques de complexité avantageuse… pour le moment!

n = 100000000
# l'élève de NSI qui ne veut pas faire Maths spécialité:

def fctA(n):
    s = 0
    for i in range(1,n+1):
        s += i
        
    return s

# --> complexité du programme = 1 + n + n + n = 3n + 1 (linéaire ==> O(n))

# vs

# l'élève qui a suivi son cours de math spécialité sur les suites:

def fctB(n):
    return n * (n + 1) // 2

# complexité = 3 (constante ==> O(1))

print ( fctA(n) ) # prend un max de temps...
print ( fctB(n) ) # quasi-immédiat !