La méthode de la fausse position, que nous allons implémenter en Python, est une méthode pour déterminer une valeur approchée de l’équation f(x) = 0.
Principe mathématique de la méthode de la fausse position(avant de l’implémenter en Python)
Introduction
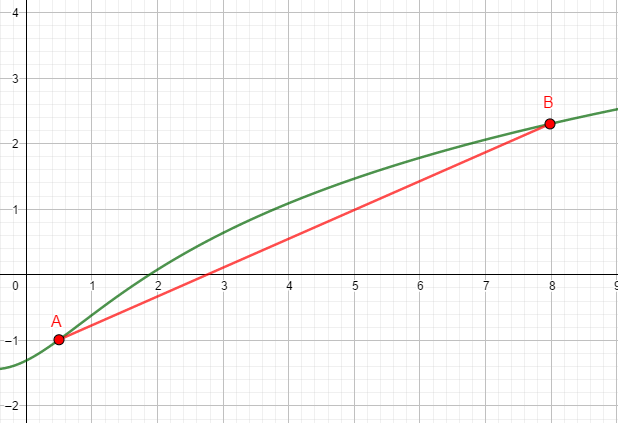
Étant donnée une fonction strictement concave ou convexe sur un intervalle donné [a ; b], on considère deux points de sa courbe représentative A(a ; f(a)) et B(b ; f(b)). On construit alors la sécante (AB).
On suppose que l’équation f(x) = 0 admet une unique solution sur [a ; b].
Alors, la sécante coupe l’axe des abscisses une unique fois en une abscisse \(x_0\). On considère alors le point \(M_0(x_0;f(x_0))\), puis la sécante \((AM_0)\) (dans notre cas).
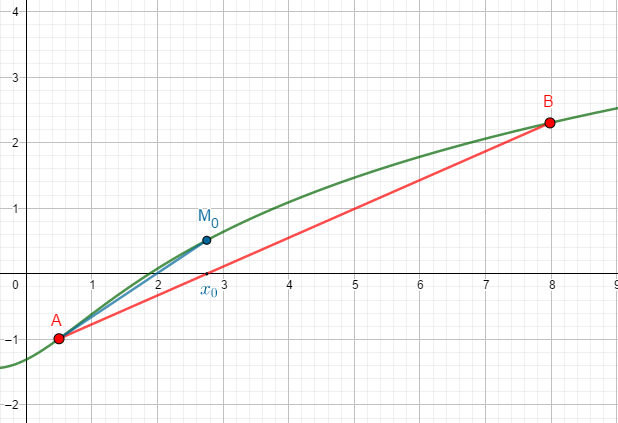
Si la fonction avait été non pas concave comme dans notre exemple mais convexe, on aurait considéré la sécante \((BM_0)\).
Cette dernière sécante coupe l’axe des abscisses en \(x_1\). On considère alors le point \(M_1(x_1;f(x_1))\) et on recommence en considérant la sécante \((AM_1)\). La suite \((x_n)\) converge alors vers la solution de l’équation f(x) = 0 qui se trouve sur [a ; b].
Relation de récurrence
Plaçons-nous dans le cas où la fonction est, comme dans l’exemple que nous venons de voir, strictement croissante et concave sur [a ; b]. Considérons alors une valeur de \(x_n\). Alors, \(x_{n+1}\) est l’abscisse de l’intersection de la sécante \((AM_n)\) avec l’axe des abscisses.
L’équation de \((AM_n)\) est de la forme y = mx + p où: $$m=\frac{f(x_n)-f(a)}{x_n-a}.$$De plus, A appartient à cette droite donc:$$f(a)=m \times a + p$$ce qui implique: $$p = f(a) – a\frac{f(x_n)-f(a)}{x_n-a}.$$On en déduit alors que l’équation réduite de \((AM_n)\) est:$$y=\frac{f(x_n)-f(a)}{x_n-a}x + f(a) – a\frac{f(x_n)-f(a)}{x_n-a}.$$
\(x_{n+1}\) est donc défini par:$$0 = \frac{f(x_n)-f(a)}{x_n-a}x_{n+1} + f(a) – a\frac{f(x_n)-f(a)}{x_n-a}$$c’est-à-dire:$$x_{n+1}=\left(a\frac{f(x_n)-f(a)}{x_n-a}-f(a)\right)\times\frac{x_n-a}{f(x_n)-f(a)}$$que l’on peut simplifier en :$$\boxed{x_{n+1}=a-\frac{x_n-a}{f(x_n)-f(a)}f(a)}$$
Implémentation de la méthode de la fausse position en Python
Une première approche
Maintenant que nous avons la relation de récurrence qui lie deux termes consécutifs de la suite \((x_n)\), on peut aisément calculer tous ces termes afin d’obtenir une valeur approchée de sa limite, qui coïncide avec la solution de l’équation f(x) = 0. Pour cela, on peut prendre \(x_0 = b\).
from math import log
def fausse_position(a,b,p):
x = a - ( b - a ) * f(a) / ( f(b) - f(a) )
while True:
t = a - ( x - a ) * f(a) / ( f(x) - f(a) )
if abs (x - t) <= 10**(-p):
return t
else:
x = t
def f(x):
return log(x*x + x + 2) - 2
print( fausse_position(0,8,10) )
qui affiche:
1.8746696820686604
Pour ce programme, j’ai importé le module math car la fonction de l’exemple pris précédemment est \(f(x)=\ln(x^2+x+2)-2\).
La fonction Python fausse_position admet trois arguments : respectivement la borne inférieure et la borne supérieure (a et b) ainsi qu’un entier p précisant la précision souhaitée (on s’arrête de faire les calculs quand deux termes consécutifs de la suite \((x_n)\) diffèrent de moins de \(10^{-p}\).
À la ligne 5, on crée une boucle « while True » qui signifie que l’on effectue les opérations de la boucle tant que « tout va bien » (pour simplifier).
La variable t joue le rôle du terme suivant dans la suite \(x_n\). Je ne pouvais pas utiliser la variable x car j’ai besoin de conserver le terme pour calculer la différence entre deux termes consécutifs (pour pouvoir arrêter la boucle quand cela est nécessaire). D’ailleurs, on le voit à la ligne 7 où je calcule |x – t|. Si je trouve une valeur plus petite que \(10^{-p}\) alors je retourne la valeur de t (qui correspond donc à la solution de l’équation f(x)=0); sinon, x devient t et je continue à « boucler ».
Pour aller plus loin
Nous l’avons vu, cette implémentation n’est valable que pour une fonction croissante et concave. Il serait donc intéressant de voir tous les cas possibles.
Si f est convexe et strictement croissante, la relation de récurrence devient:$$x_0 = a,\ x_{n+1}=b – \frac{b-x_n}{f(b)-f(x_n)}f(b).$$ On peut alors compléter le programme précédent:
from math import exp
def fausse_position(a,b,p,concave = True):
if concave == True:
x = b
else:
x = a
while True:
if concave == True:
t = a - ( x - a ) * f(a) / ( f(x) - f(a) )
else:
t = b - (b - x) * f(b) / ( f(b) - f(x) )
if abs (x - t) <= 10**(-p):
return t
else:
x = t
def f(x):
return exp(x - 2) - 2
print( secante(0,8,10,concave=False) )
qui affiche bien la solution de l’équation \(\text{e}^{x-2}-2=0\) sur [0;8]:
2.693147176947308
J’ai en effet changé la fonction pour prendre une fonction convexe.
Si l’on regarde maintenant le cas d’une fonction strictement décroissante et concave, le « point de référence » est B donc \(x_0=a\) et la relation de récurrence est la même que pour une fonction convexe et croissante. On a donc les équivalences:$$\text{décroissante concave} \iff \text{croissante convexe}$$ce qui induit le programme suivant:
def fausse_position(a,b,p,concave = True):
# variation de la fonction
if f(a) > f(b):
croissante = False
else:
croissante = True
# convexité de la fonction
if (concave == True and croissante == True) or (concave == False and croissante == False):
x = b
else:
x = a
# calculs
while True:
if (concave == True and croissante == True) or (concave == False and croissante == False):
t = a - ( x - a ) * f(a) / ( f(x) - f(a) )
else:
t = b - (b - x) * f(b) / ( f(b) - f(x) )
if abs (x - t) <= 10**(-p):
return t
else:
x = t
Je suppose bien entendu ici que la fonction est strictement monotone sur l’intervalle.
Cette méthode ressemble de près à la méthode de la sécante; il ne faut donc pas les confondre.
N’oubliez pas que si vous avez des difficultés en mathématiques, je peux vous aider par webcam.