La méthode de Newton est une des méthodes algorithmiques de résolution d’équations. Elle vient palier au défaut majeur de la dichotomie, à savoir sa « lenteur ». Quel en est le principe ? Comment l’implémenter en Python ?

Principe mathématique de la méthode de Newton
On considère une fonction f continue et dérivable sur un intervalle [a ; b]. On pose alors \(x_0 = a\) et \(A_0(x_0;f(x_0))\) en lequel on trace une tangente.
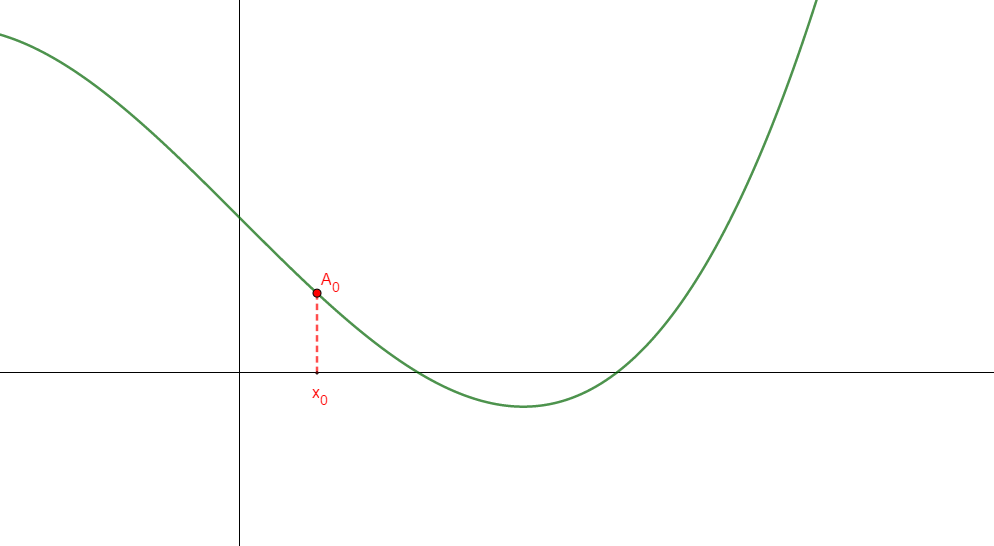
Cette tangente coupe l’axe des abscisses en un point d’abscisse notée \(x_1\):
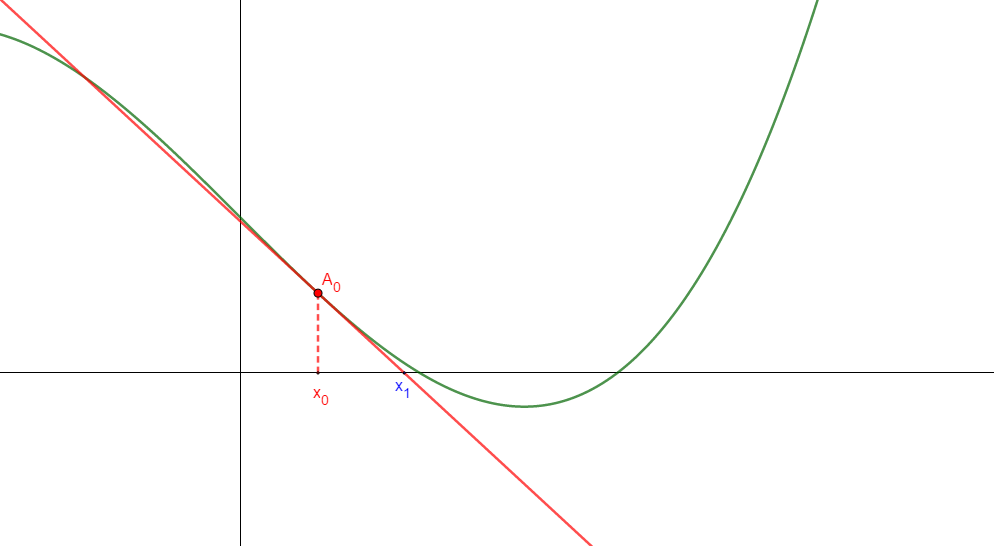
On considère alors le point \(A_1(x_1;f(x_1))\) en lequel on trace la tangente à la courbe:
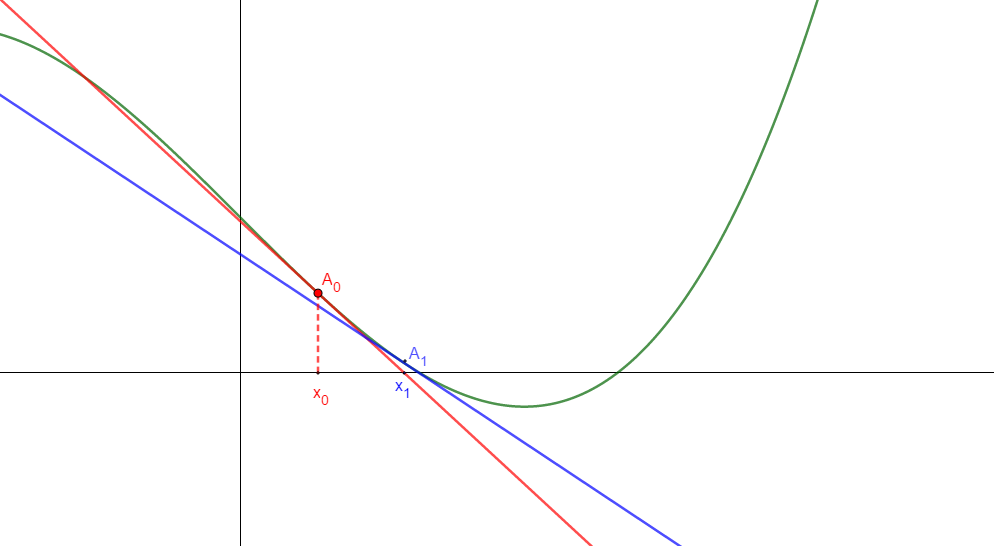
Cette tangente coupe l’axe des abscisses en un point d’abscisse \(x_2\). On considère alors le point \(A_2(x_2;f(x_2))\) en lequel on trace la tangente à la courbe, qui coupe l’axe des abscisses en \(x_3\), etc.
On construit ainsi une suite de nombre sur l’axe des abscisses qui se rapprochent de la solution de l’équation : le point d’intersection de la courbe et de l’axe des abscisses.
La suite numérique définie par la méthode de Newton
Considérons un point \(A_n(x_n;f(x_n))\) ; l’équation de la tangente en ce point est:$$y=f'(x_n)(x-x_n)+f(x_n)$$et \(x_{n+1}\) est donc défini comme la solution de l’équation :$$0=f'(x_n)(x_{n+1}-x_n) + f(x_n)$$ soit: $$x_{n+1} = -\frac{f(x_n)}{f'(x_n)}+x_n.$$Il faut donc, pour que cette méthode fonctionne, que tous les \(f'(x_n)\) soient non nuls sur l’intervalle considéré.
Ainsi, nous allons considérer la suite \(x_n\) définie par:$$\begin{cases}x_0=a\\x_{n+1}=-\frac{f(x_n)}{f'(x_n)}+x_n\end{cases}$$
Implémentation en Python
Une fois la suite définie, il n’y a rien de bien compliqué dans l’implémentation en Python de la méthode:
def newton(fonction,derivee,a,e):
delta = 1
while delta > e:
x = -fonction(a)/derivee(a) + a
delta = abs(x - a)
a = x
return x , delta
print( newton(lambda x: 0.1*x**3-x+1 , lambda x: 0.3*x**2-1 , 0 , 0.001) )
La fonction newton admet quatre arguments:
- fonction représente la fonction f ;
- derivee représente la fonction dérivée de la fonction f ;
- a représente la valeur initiale de la suite;
- e représente l’erreur maximale souhaitée.
J’ai choisi ici d’écrire les fonctions à l’aide de l’opérateur Python lambda car je trouve cela plus sympa, mais on peut aussi définir les fonctions autrement:
def newton(a,e):
delta = 1
while delta > e:
x = -fonction(a)/derivee(a) + a
delta = abs(x - a)
a = x
return x , delta
def fonction(x):
return 0.1*x**3-x+1
def derivee(x):
return 0.3*x**2-1
print( newton(0 , 0.001) )
Certains préfèreront ce dernier script car plus facile à comprendre (plus intuitif). Notez que si on définit les fonctions comme ceci, nul besoin de les mettre en arguments de la fonction newton; la syntaxe de cette dernière est donc plus allégée.
Vitesse de convergence
La vitesse de convergence d’une suite est déterminée à l’aide d’une majoration de la forme:$$|x_n-\alpha|\leqslant v_n$$où \(v_n\) est une suite numérique et \(\alpha\) la limite de la suite \(x_n\).
Pour cette méthode, on arrive à démontrer que:$$|x_n-\alpha|\leqslant \big[ k|x_0-\alpha| \big]^{2^n},$$où \(k\) est une constante, ce qui est considéré comme une vitesse très rapide; on dit ici que la vitesse est quadratique, c’est-à-dire que la précision de l’approximation double à chaque étape contrairement à la dichotomie qui a une vitesse de convergence linéaire, c’est-à-dire où \(|x_n-\alpha|\leqslant q^n\).
Pour les plus curieux, si I est un intervalle compact contenant les \(x_n\) et \(\alpha\), et inclus dans le domaine de définition de f, $$k=\frac{\max_{x\in I}|f^{\prime\prime}(x)|}{2\min_{x\in I}|f^\prime(x)|}.$$Mais ce n’est pas du tout au programme du lycée!
Et n’oubliez pas que si vous avez des problèmes en maths, je peux vous aider webcam (cours ponctuels ou réguliers).
super intéressant
parfait ! Le code fonctionne à merveille. Je peux duper ma prof de mathématiques en faisant croire que c’est moi
Bonjour, je suis étudiant férue au sein du lycée saint jean de passy. J’étudie le python et ce site m’a agréablement surpris par sa qualité d’écriture. Le professeur nous avais demandé de faire un code python ici et j’ai pu tout copier à la moindre ligne en comprenant la moitié.. Cela m’a permis de me relaxer traaaaannnnquiiiillement pendant que mes camarades continuaient à se trotter la binette !
Je tenais à vous remercier pour la qualité de votre travail ! 4.999999 (infii de 9)/5 (ssous entendu c(est comme si c’était 5/5) ; )