![]()
Les bases en Python (binaire, hexadécimale et décimale) ne font que traduire le système de numération que nous utilisons de nos jours, qui n’est que la résultante d’une histoire. Nous comptons en base 10 car nous avons 10 doigts, mais en Mésopotamie, berceau des civilisations et des mathématiques, on comptait en base sexagésimale.
La base sexagésimale
En Mésopotamie, il fallait compter jusqu’à plus de 10 pour savoir combien de bêtes on avait ou on voulait vendre. Dix doigts, ce n’était pas très pratique… Aussi, on utilisait les phalanges.
Prenons la main droite et servons-nous du pouce pour compter les phalanges des quatre autres doigts:
Nous arrivons jusqu’à 12. On peut alors lever le pouce de la main gauche et repartir pour compter à nouveau jusqu’à 12 avec la main droite. Une fois arrivés à la deuxième douzaine, on peut lever l’index gauche pour désigner le fait que l’on a compté 2 douzaines. Comme la main gauche a 5 doigts (enfin, en général…), on peut alors compter jusqu’à \(5 \times 12=60\). « 60 » est donc la base de la numération mésopotamienne, la base sexagésimale. D’ailleurs, ne vous êtes-vous jamais demandés pourquoi il y a 60 minutes dans une heure et 60 secondes dans une minute ? Pourquoi l’angle plein mesure-t-il 360°, c’est-à-dire 6 fois 60 ? Cela vient de cette base.
La numération mésopotamienne est basée sur le système de position. Nous allons expliquer cela.
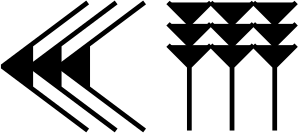
Un clou représente une unité (1).
Un chevron représente 10 unités (10). Bien que raisonnant en base sexagésimale, il semblerait que le dizaine ait une importance dès cette ère.
Ainsi, pour écrire « 39 », ils utilisaient ces symboles en adoptant la convention que ce qui est le plus à gauche est le plus important (comme dans notre système de numération) :
La base décimale
Si on analyse ce qui précède, on voit que les symboles représentent:$$3\times10+9\times1$$que l’on peut aussi voir comme étant:$$3\times10^1 + 9\times10^0.$$Et par extension, n’importe quel nombre s’écrivant \(a_na_{n-1}a_{n-2}\cdots a_0\) peut s’écrire:$$a_n\times10^n + a_{n-1}\times10^{n-1} + a_{n-2}\times10^{n-2}+\cdots+a_1\times10^1 + a_0\times10^0=\sum_{p=0}^n a_p\times10^p.$$On écrira alors:$$\overline{a_n\cdots a_0}^{10}=\sum_{p=0}^n a_p\times10^p.$$
La base hexadécimale
Ce que l’on a fait pour 10, on peut le faire pour d’autres nombres. On peut donc imaginer une base 16, appelée hexadécimale (hexa = « six », décimale = « dix », hexadécimale = 6 + 10 = 16).
Comme nous n’avons que 10 symboles pour représenter des chiffres, il faudra utiliser des lettres pour les 6 manquants : A, B, C, D, E et F représenteront alors respectivement 10, 11, 12, 13, 14 et 15. Sur le même principe que dans le système décimal, les symboles les plus à gauche représentent les plus grandes puissances de 16.
Par exemple,$$\overline{A58E}^{16} = 10\times16^3 + 5\times16^2 + 8\times16^1 + 14\times16^0=42382.$$Cette base est utilisée pour représenter les couleurs en informatique.
Le binaire
C’est la base qui ne comporte que deux symboles : « 0 » et « 1 ».
Si nous voulons savoir quel nombre (décimal) représente « 1100101 », il suffit de l’imaginer dans un tableau comme celui-ci par exemple:
| \(2^6\) | \(2^5\) | \(2^4\) | \(2^3\) | \(2^2\) | \(2^1\) | \(2^0\) |
| 1 | 1 | 0 | 0 | 1 | 0 | 1 |
ce qui donne:$$\overline{1100101}^2 = 2^6 + 2^5 + 2^2 + 2^0 = 101.$$On n’additionne ici que les puissances de 2 où il y a un « 1 ».
Conversion de la base décimale à l’hexadécimal en Python
C’est le cas le plus simple car il y a une fonction dédiée à cela:
hex(42382)
'0xa58a'
Vous constaterez que le résultat (a58e) est précédé de « 0x » pour spécifier que cela représente un hexadécimal.
On peut aussi utiliser la fonction format:
format(42382,'#x') format(42382,'x')
'0xa58e' 'a58e'
Notez que la deuxième solution supprime le préfixe « 0x ».
Conversion de la base décimale au binaire en Python
Là encore, il y a une fonction :
bin(101)
'0b1100101'
Le résultat (1100101) est cette fois-ci précédée de « 0b » pour spécifier que c’est un binaire.
On peut aussi utiliser la fonction format:
format(101,'#b') format(101,'b')
'0b1100101' '1100101'
Constatez que l’on peut directement avoir le binaire sans le préfixe « 0b ».
Conversion de la base décimale en binaire et en hexadécimal avec Python
Nous pouvons encore utiliser la fonction format:
format(0b1011001,'d')
'89'
Ici, nous avons convertit le binaire \(\overline{1011001}^2\) en décimal.
format(0xa45bc,'d')
'673212'
Nous avons ici convertit l’hexadécimal \(\overline{a45bc}^{16}\) en décimal.
Dans mon livre de NSI niveau 1ère, je présente plusieurs programmes Python pour les conversions. C’est un bon entraînement pour celles et ceux souhaitant s’initier sérieusement à ce langage, mais à l’avenir, il est préférable d’utiliser la fonction format pour toute conversion.
Attention toutefois : les résultats sont de type str (chaîne de caractères); ce ne sont pas des nombres (et pour cause !).