En Terminale NSI, il est question de graphes et de leur implémentation en Python. Cet outil mathématique, combiné à l’informatique, permet par exemple de gérer des réseaux (routiers ou informatiques), de construire des labyrinthes, de représenter et d’étudier des flux migratoires, ou plus généralement, des changements d’états. C’est donc une notion très importante.
Les graphes en Python, une notion avant tout mathématique
Une brève histoire
La notion de graphes semble apparaître pour la première fois dans un article du mathématicien suisse Leonhard Euler parut en 1735, dans lequel il se penchait sur le « problème des ponts de Königsberg », ville représentée avec ses ponts sur le schéma suivant:
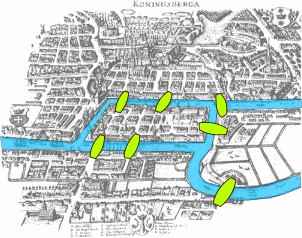
Ce problème consistait à « trouver une promenade à partir d’un point donné qui fasse revenir à ce point en passant une fois et une seule par chacun des sept ponts de la ville de Königsberg » (source : https://fr.wikipedia.org/wiki/Th%C3%A9orie_des_graphes).
Par la suite, toujours au XVIIIème siècle, le mathématicien français Alexandre-Théophile Vandermonde se pencha sur le problème du cavalier devant visiter toutes les cases d’un échiquier, problème résoluble à l’aide de la théorie des graphes.
Mais qu’est-ce qu’un graphe ?
Un graphe est un couple \(\mathcal{G} = ( V ; E )\), où V est un ensemble fini d’éléments, appelés les sommets du graphe (« V » comme vertex, autrement dit sommets) et E l’ensemble des connexions entre les sommets, que l’on nomme aussi les arêtes du graphe (« E » comme edges, dans le sens de arêtes).
Par exemple, $$\mathcal{G} = ( \{ A; B;C\} ; \{(A,B);(A,C);(B,C) \} )$$ peut désigner le graphe ayant trois sommets : A, B et C, où A et B, A et C ainsi que B et C sont reliés.
À quoi ça peut servir ?
Les graphes servent à représenter des situations diverses. Cela peut être des:
- villes (sommets) et leurs flux migratoires (arêtes);
- intersections de rues (sommets) et des rues (arêtes);
- cases de labyrinthes (sommets) et leurs connexions (arêtes), le fait de pouvoir passer d’une case à l’autre;
- états d’un individu (sommets), comme « fatigué », « stressé », « calme », …) et le passage d’un état à l’autre (arêtes);
- etc.
Vous l’aurez peut-être compris, dans certaines situations, deux sommets peuvent être reliés par une arête avec ou sans orientation. Le simple fait de donner le couple \(\mathcal{G} = ( V ; E )\) peut donc être ambiguë, d’où la nécessité d’introduire une représentation graphique.
Représentation sagittale
On nomme donc représentation sagittale la représentation graphique d’un graphe; quand les arêtes doivent avoir une orientation, on parlera de graphes orientés. Dans ce cas, on parlera plutôt d’arcs et non d’arêtes.
Mais il arrive aussi que l’on doive attribuer à certaines arrêtes une pondération (un nombre). Par exemple, une probabilité (quand il s’agit de passer d’un état à un autre), une distance ou encore un temps (quand les arêtes représentent une connexion entre deux lieux géographiques par exemple). On parle alors de graphes pondérés ou de graphes probabilistes.
Les pondérations, les nombres qu’il y a sur chaque arc, peuvent représenter des:
- distances (si les sommets représentent des lieux géographiques par exemple);
- temps (temps de parcours pour aller d’un sommet à un autre);
- débits (dans le cas d’un graphe représentant un réseau informatique);
- probabilités (de changement d’état; par exemple, probabilité de passer d’un état « anxieux » à un état « euphorique ») comme sur la figure ci-dessous;
- etc.
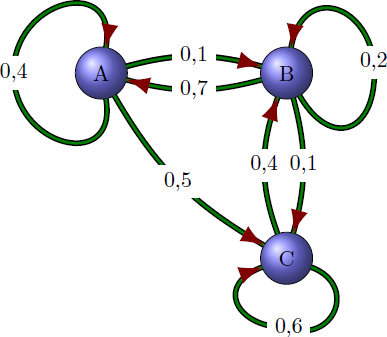
où, par exemple, la probabilité de passer de l’état « A »
à l’état « C » est égale à 0,5
Matrice d’un graphe
Quel que soit le type de graphe, qu’il soit orienté ou pas, pondéré ou non, il admet toujours une représentation matricielle.
Une matrice est un tableau de nombres, représenté entre parenthèses et sans trait de délimitation. Quand une matrice représente une graphe, chaque ligne et colonne représente un sommet. La matrice est alors appelée matrice d’adjacence du graphe.
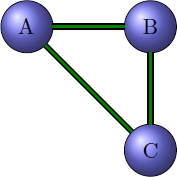
Par exemple, le graphe suivant:

admet pour matrice d’adjacence:
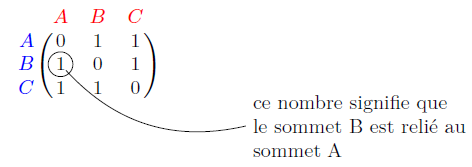
Quand deux sommets i et j sont reliés par une arêtes, on met un « 1 » à l’intersection de la ligne i et de la colonne j. Dans le cas contraire, on met un « 0 ».
Remarquez que quand le graphe est non orienté, la matrice est symétrique (par rapport à la diagonale principale, celle qui part du haut à gauche et qui va en bas à droite, diagonale qui ne comporte que des « 0 »).
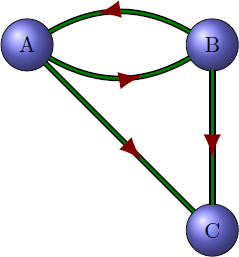
La matrice du graphe suivant:

est:

Ici, le sens (l’orientation des arcs) à une importance; il est donc normal que la matrice ne soit plus symétrique par rapport à la diagonale principale.
Quand il s’agit de graphes pondérés, on ne met plus uniquement de « 0 » et de « 1 », mais on y met les pondérations. Le graphe suivant:
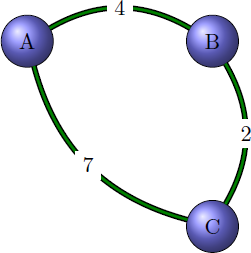
admet alors pour matrice d’adjacence:

Pour le graphe suivant:

sa matrice d’adjacence est:
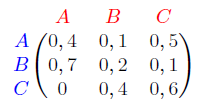
Ici, la somme des coefficients de chaque ligne doit valoir « 1 » (somme des probabilités « partantes » d’un sommet).
Deux exemples d’application de graphes
Labyrinthes
Un labyrinthe peut être vu comme un plateau décomposé en cases avec quelques traits de séparation. Dans ce cas, le labyrinthe peut être représenté par un graphe où chaque sommet représente une case du « tableau » et où chaque arête représente le fait que l’on peut passer d’une case à l’autre car il n’y a pas de mur qui l’en empêche.
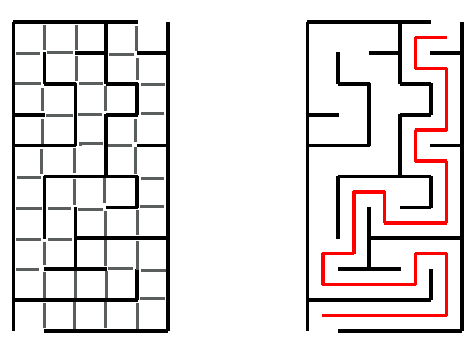
C’est d’ailleurs ainsi que j’ai programmé mon logiciel pour construire des labyrinthe (voir cette page).
Changements d’états
Supposons que la matrice suivante représente des changements d’états:

On peut par exemple imaginer que A, B et C sont respectivement les états:
- A : « fatigué »
- B : « motivé »
- C : « neutre »
d’un individu. Supposons alors cet cet individu soit initialement fatigué (état A). On nomme alors:$$E_0=\begin{pmatrix}1 &0&0\end{pmatrix}$$ la représentation matricielle de cet état initial.
Supposons maintenant qu’une observation de l’état soit faite toute les heures. Alors, si \(M\) est la matrice d’adjacence du graphe, l’état probabiliste au bout d’une heure est donné par:$$E_1 = E_0 \times M = \begin{pmatrix}0,4 & 0,1 & 0,5 \end{pmatrix}.$$Une heure après, on se retrouve avec un état représenté par:$$E_2 = E_1 \times M = E_0 \times M^2 = \begin{pmatrix}0,23 & 0,26 & 0,51\end{pmatrix}.$$Ainsi, si l’on veut savoir l’état à très long terme, on calcule:$$E_\infty = E_0 \times M^\infty \approx \begin{pmatrix}0,3 & 0,26 & 0,44\end{pmatrix}.$$Cet état nous donne les probabilités d’être dans les états A, B et C. Ici, à long terme, on a par exemple 3 chances sur 10 d’être dans l’état A.
Quand le graphe est pondéré et que les pondérations représentent non plus des probabilités mais des nombres (comme des distances ou du temps), la matrice d’adjacence peut nous permettre de trouver le plus court chemin pour relier deux sommets, c’est-à-dire le chemin dont la somme des pondérations est minimal. Un algorithme connu est celui de Dijkstra. C’est d’ailleurs cet algorithme qui est utilisé par les routeurs pour trouver le chemin le plus rapide, donc qui nécessite le moins de temps de transmission.
Vous comprendrez donc que les matrices d’adjacence permettent de voir de façon abstraite des graphes et donc de les implémenter dans un programme informatique.
Implémentation de graphes en Python
Les graphes peuvent être implémentés en Python de plusieurs façon. J’en ai choisi deux.
Approche naïve (mais simple)
Une approche naïve serait de considérer un graphe comme un dictionnaire, où les clés sont les sommets et les valeurs, les sommets reliés aux clés. Cela donnerait par exemple:
G = {
'A' : ('B' , 'C') ,
'B' : ('A' , 'C'),
'C' : ('A' , 'B')
}
qui représente le graphe:

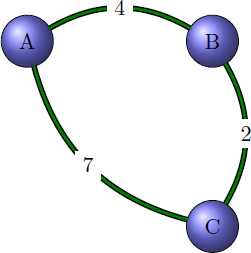
Pour les graphes pondérés, on peut imaginer quelque chose qui ressemble à ça:
G = {
'A' : ( {'B':4} , {'C':7} ) ,
'B' : ( {'A':4} , {'C':2} ),
'C' : ( {'A':4} , {'B':2} )
}
qui représente le graphe:

Ce genre d’implémentation est nommée implémentation par liste d’adjacence de graphes en Python.
Une autre façon d’implémenter des graphes en Python est d’utiliser leur matrice d’adjacence. Ainsi, pour le premier graphe, on aura:
G = [ [ 0 , 1 , 1 ] , [ 1 , 0 , 1 ] , [ 1 , 1 , 0 ] ]
L’inconvénient d’une telle implémentation réside dans l’espace mémoire dédié au graphe. En effet, pour un graphe à n sommets, il faut une matrice avec n² nombres… et la plupart du temps, il y a beaucoup de « 0 » (on parle de matrices creuses), ce qui est ballot non ?
Dans ce cas, l’implémentation par liste d’adjacence est bien mieux car nécessite moins d’espace mémoire.
Des graphes en Python sont des objets
Un graphe n’est autre qu’une représentation d’une situation; c’est donc un objet abstrait… Et en informatique, il existe un paradigme de programmation permettant d’implémenter de telles notions : la Programmation Orientée Objet (POO pour les intimes). Ce paradigme colle parfaitement à l’implémentation des graphes, même si c’est un peu plus compliqué que l’approche naïve.
Selon ce paradigme, un objet est représenté par une classe, contenant idéalement un constructeur et des méthodes.
Le constructeur
C’est la « fonction interne » à la classe, à l’objet, qui définit pour cet objet, et lui seulement, d’éventuels paramètres.
Prenons un exemple de graphe non orienté et non pondéré (pour faire simple). On peut alors imaginer que l’on déclare un graphe (le premier par exemple) sous la forme:
G = Graphe( ('A','B') , ('A','C') , ('B','C') )
Dans ce cas, on peut imaginer un constructeur de la manière suivante:
class Graphe:
def __init__(self,*args):
self.edges = [ e for e in args ]
self.nodes = []
for e in self.edges:
if e[0] not in self.nodes:
self.nodes += [ e[0] ]
if e[1] not in self.nodes:
self.nodes += [ e[1] ]
G = Graphe( ('A','B') , ('A','C') , ('B','C') )
print( 'Les noeuds de G sont : {}'.format(G.nodes) )
print( 'Les arêtes de G sont : {}'.format(G.edges) )
On a ici définit un constructeur qui construit une liste des nœuds du graphe et une liste contenant toutes les arêtes.
Méthodes de la classe
À ce constructeur, on peut ajouter à notre classe une méthode permettant d’avoir la matrice d’adjacence:
class Graphe:
def __init__(self,*args):
self.edges = [ e for e in args ]
self.nodes = []
for e in self.edges:
if e[0] not in self.nodes:
self.nodes += [ e[0] ]
if e[1] not in self.nodes:
self.nodes += [ e[1] ]
def mat(self):
self.mat = [[ 0 for j in range(len(self.nodes))] for i in range(len(self.nodes))]
for i in self.edges:
self.mat[ self.nodes.index(i[0]) ][ self.nodes.index(i[1]) ] = 1
self.mat[ self.nodes.index(i[1]) ][ self.nodes.index(i[0]) ] = 1
return self.mat
G = Graphe( ('A','B') , ('A','C') , ('B','C') )
print( 'Les noeuds de G sont : {}'.format(G.nodes) )
print( 'Les arêtes de G sont : {}'.format(G.edges) )
print( 'La matrice d\'adjacence de G est : {}'.format(G.mat()) )
La façon d’implémenter un graphe n’est pas unique : elle dépend de notre façon de voir les choses mais aussi de ce que l’on veut en faire. Aussi, la classe que je viens de vous montrer n’est pas unique. D’ailleurs, dans le livre de Terminale NSI que j’ai co-écrit, j’utilise d’autres manières.
Il est bien connu que chaque script ressemble à son créateur… Donc vous pouvez imaginer votre propre classe Graphe d’une autre façon.
Dans ce livre, co-écrit avec un véritable informaticien en exercice, vous trouverez un cours plus complet.
