Un arbre fractal de Pythagore est une figure plutôt esthétique dans certaines conditions.
Nous allons voir ce que c’est…
Je précise que cet article est rédigé en s’appuyant sur la vidéo de Mickaël Launay visible sur Youtube.
Notion de similitude
Considérons:
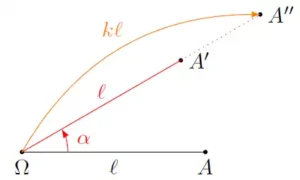
- un point \(\Omega\) du plan,
- un réel \(k\),
- un ange $\alpha$.
À tout point $A$ du plan, on peut considérer successivement:
- son image $A’$ par la rotation de centre $\Omega$ et d’angle $\alpha$,
- puis $A”$ l’image de $A’$ par l’homothétie de centre $\Omega$ et de rapport $k$.
À l’aide de la trigonométrie, on démontre que: $$\left.\begin{array}{l}\Omega(x_\Omega;y_\Omega)\\A(a;b)\end{array}\right\rbrace \Longrightarrow\begin{cases}A'(x_\Omega+(a-x_\Omega)\cos\alpha-(b-y_\Omega)\sin\alpha; y_\Omega+(a-x_\Omega)\sin\alpha+(b-y_\Omega)\cos\alpha)\\A”(x_\Omega + k(a-x_\Omega)\cos\alpha-k(b-y_\Omega)\sin\alpha;y_\Omega+k(a-x_\Omega)\sin\alpha+k(b-y_\Omega)\cos\alpha)\end{cases}$$
On dit ici que $A”$ est obtenu à partir du point $A$ par similitude de centre $\Omega$, d’angle $\alpha$ et de rapport $k$.
Introduction à l’arbre de Pythagore
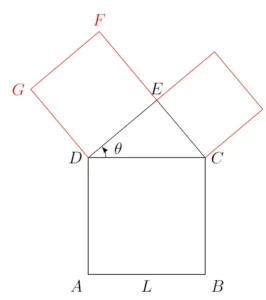
Partons d’un carré $ABCD$ de côté $L$, puis traçons un triangle rectangle $ECD$ tel que $\widehat{CDE}=\theta$, sur lequel nous traçons des carrés:
- $E$ est obtenu par similitude de centre $D$, d’angle $\theta$ et de rapport $k=L\cos\theta$ car $\dfrac{DE}{DC}=\cos\theta$.
- $F$ est obtenu à partir de $D$ par rotation de centre $E$ et d’angle $-\frac{\pi}{2}$.
- $G$ est obtenu à partir de $E$ par rotation de centre $D$ et d’angle $\frac{\pi}{2}$.
On peut construire de même le carré sur $|EC]$.
Construction de l’arbre de Pythagore
L’idée est de reproduire ce qui vient d’être expliqué sur les carrés obtenus, et sur ceux qui vont l’être par la suite. Nous allons faire cela à l’aide de Python:
from math import pi, cos, sin
from PIL import Image, ImageDraw
width = 1748
height = 1240
tree = Image.new('RGB', (width,height), (255,255,255))
draw = ImageDraw.Draw(tree,'RGBA')
theta = pi/180 * 40 # 40 degrés
L = 200 # longueur de l'arête du premier carré
A = (width/2 - L/2 , height-250)
B = (width/2 + L/2 , height-250)
def sim(centre, point, angle, k):
# angle devient "-angle" dans les sinus à cause de la logique graphique de PIL
x = centre[0] + k*(point[0]-centre[0])*cos(angle)-k*(point[1]-centre[1])*sin(-angle)
y = centre[1] + k*(point[0]-centre[0])*sin(-angle)+k*(point[1]-centre[1])*cos(angle)
return x,y
def arbre(A,B,angle,n):
if n==0: return
C = sim(B,A,-pi/2,1)
D = sim(A,B,pi/2,1)
E = sim(D,C,angle,cos(angle))
draw.polygon([A,B,C,D], fill=(0,0,0,125))
arbre(D, E, angle, n-1)
arbre(E, C, angle, n-1)
arbre(A,B,theta,10)
tree.show()
Si l’on souhaite mettre un peu de couleur, on peut utiliser le script suivant:
from math import pi, cos, sin
from PIL import Image, ImageDraw
from random import randint
width = 1748
height = 1240
tree = Image.new('RGB', (width,height), (255,255,255))
draw = ImageDraw.Draw(tree,'RGBA')
theta = pi/180 * 40 # 40 degrés
L = 200 # longueur de l'arête du premier carré
A = (width/2 - L/2 , height-250)
B = (width/2 + L/2 , height-250)
def sim(centre, point, angle, k):
# angle devient "-angle" dans les sinus à cause de la logique graphique de PIL
x = centre[0] + k*(point[0]-centre[0])*cos(angle)-k*(point[1]-centre[1])*sin(-angle)
y = centre[1] + k*(point[0]-centre[0])*sin(-angle)+k*(point[1]-centre[1])*cos(angle)
return x,y
def arbre(A,B,angle,n):
if n==0: return
C = sim(B,A,-pi/2,1)
D = sim(A,B,pi/2,1)
E = sim(D,C,angle,cos(angle))
draw.polygon([A,B,C,D], fill=(randint(0,255),randint(0,255),randint(0,255),125))
arbre(D, E, angle, n-1)
arbre(E, C, angle, n-1)
arbre(A,B,theta,10)
tree.show()
L’arbre est-il “infini” ?
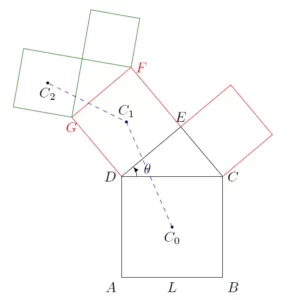
Nous allons noter $C_n$ le centre des carrés allant vers la gauche.
On peut observer que $$\frac{C_2C_1}{C_1C_0}=\cos\theta.$$ En effet, $DEFG$ est l’image de $ABCD$ ($DC$ se transforme en $DG$) par la similitude de centre $D$, d’angle $\theta+\frac{\pi}{2}$ et de rapport $k=\cos\theta$ (par construction). De même, le carré vert est l’image du carré rouge par la similitude de centre $G$ et de mêmes angles et rapport.
Toutes les longueurs sont donc multipliées par $\cos\theta$ pour passer d’un carré au suivant.
La suite $(C_{n-1}C_n)$ est donc géométrique de raison $\cos\theta$.
Calculons alors longueur:$$\begin{align*}L_n & = \sum_{k=0}^{n-1} C_kC_{k+1}= C_0C_1 + C_1C_2 + \cdots + C_{n-1}C_{n}\\& = C_0C_1 \times (1 + \cos\theta + \cos^2\theta + \cdots + \cos^n\theta)\\& = C_0C_1\times\dfrac{1-\cos^{n+1}\theta}{1-\cos\theta}.\end{align*}$$
Comme $0 \leqslant \cos\theta < 1$, la limite de $L_n$ quand $n$ tend vers $+\infty$ est finie et vaut $\frac{C_0C_1}{1-\cos\theta}$.
L’arbre de Pythagore (noté $\mathcal{A}$) ne peut donc pas être \og infini \fg{} (dans le sens où la distance entre $C_0$ et $C_\infty$ ne peut pas être infinie).
Je vais appeler plus grand rayon (PGR), et je vais le noter $\mathcal{PGR}(\mathcal{A})$ le maximum de la distance entre $C_0$ et $C_n$, pour tout entier naturel $n$: $$\mathcal{PGR}(\mathcal{A})=\max\{C_0C_n,\ n\geqslant1\}.$$
On peut ainsi modifier le script précédent pour déterminer une valeur approchée du PGR (en pixels) de l’arbre:
from math import pi, cos, sin
from PIL import Image, ImageDraw, ImageFont
from random import randint
width = 1748
height = 1240
tree = Image.new('RGB', (width,height), (255,255,255))
draw = ImageDraw.Draw(tree,'RGBA')
theta = pi/180 * 40 # 40 degrés
L = 200 # longueur de l'arête du premier carré
A = (width/2 - L/2 , height-250)
B = (width/2 + L/2 , height-250)
centres = []
def sim(centre, point, angle, k):
# angle devient "-angle" dans les sinus à cause de la logique graphique de PIL
x = centre[0] + k*(point[0]-centre[0])*cos(angle)-k*(point[1]-centre[1])*sin(-angle)
y = centre[1] + k*(point[0]-centre[0])*sin(-angle)+k*(point[1]-centre[1])*cos(angle)
return x,y
def arbre(A,B,angle,n):
if n==0: return
global centres
C = sim(B,A,-pi/2,1)
D = sim(A,B,pi/2,1)
E = sim(D,C,angle,cos(angle))
centres.append(((A[0]+C[0])/2,(A[1]+C[1])/2))
draw.polygon([A,B,C,D], fill=(randint(0,255),randint(0,255),randint(0,255),125))
arbre(D, E, angle, n-1)
arbre(E, C, angle, n-1)
def pgr():
global centres
origine = centres[0] # premier centre
d = 0
for c in centres:
if c != origine:
distance = (origine[0]-c[0])**2 + (origine[1]-c[1])**2
if distance > d:
d = distance
faraway = c
return d**0.5, faraway
arbre(A,B,theta,15)
pgr = f"PGR de l'arbre: {pgr()[0]}"
draw.text((10,10), pgr, font=ImageFont.truetype("arial.ttf", size=30), fill=(0, 0, 0, 255))
# on trace le PGR
draw.line([centres[0],pgr()[1]],fill=(100,100,100),width=1)
tree.show()
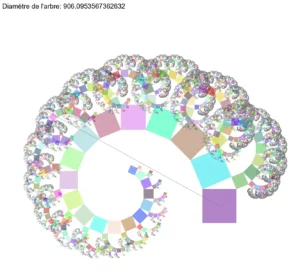
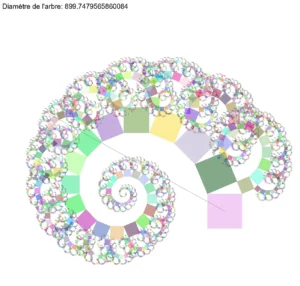
Lors de la rédaction de cet article, j’ai appelé “diamètre” ce que j’appelle actuellement “PGR”. Cette terminologie me semblant trompeuse, je l’ai changé pour “PGR”, mais n’ai pas pris le temps de refaire les images. C’est pourquoi vous pouvez lire “Diamètre” et non “PGR”. Il en sera de même pour les images suivantes.
Ce dernier exemple est intéressant (j’ai pris $n=20$ et un angle initial de 22.5 degrés): on aimerait que le nombre d’itérations soit plus grand afin que la “spirale” continue davantage… Nous allons donc légèrement modifier le script afin de le permettre car avec ce que nous avons, pour $n=25$, ça plante…
from math import pi, cos, sin
from PIL import Image, ImageDraw, ImageFont
from random import randint
width = 1748
height = 1240
tree = Image.new('RGB', (width,height), (255,255,255))
draw = ImageDraw.Draw(tree,'RGBA')
theta = pi/180 * 22.5
L = 150 # longueur de l'arête du premier carré
A = (width/2 - L/2 +100, height-250)
B = (width/2 + L/2 +100, height-250)
centres = []
def sim(centre, point, angle, k):
# angle devient "-angle" dans les sinus à cause de la logique graphique de PIL
x = centre[0] + k*(point[0]-centre[0])*cos(angle)-k*(point[1]-centre[1])*sin(-angle)
y = centre[1] + k*(point[0]-centre[0])*sin(-angle)+k*(point[1]-centre[1])*cos(angle)
return x,y
def arbre(A,B,angle,n):
if (n==0) or (length(A,B)<8): return
global centres
C = sim(B,A,-pi/2,1)
D = sim(A,B,pi/2,1)
E = sim(D,C,angle,cos(angle))
centres.append(((A[0]+C[0])/2,(A[1]+C[1])/2))
draw.polygon([A,B,C,D], fill=(randint(0,255),randint(0,255),randint(0,255),125))
arbre(D, E, angle, n-1)
arbre(E, C, angle, n-1)
def length(A,B):
return (A[0]-B[0])**2 + (A[1]-B[1])**2
def pgr():
global centres
origine = centres[0] # premier centre
d = 0
for c in centres:
if c != origine:
distance = length(origine,c) #(origine[0]-c[0])**2 + (origine[1]-c[1])**2
if distance > d:
d = distance
faraway = c
return d**0.5, faraway
arbre(A,B,theta,50)
pgr = f"PGR de l'arbre: {pgr()[0]}"
draw.text((10,10), pgr, font=ImageFont.truetype("arial.ttf", size=30), fill=(0, 0, 0, 255))
draw.line([centres[0],pgr()[1]],fill=(100,100,100),width=1)
tree.show()
Nous avons introduit:
- une nouvelle fonction “length” qui permet de renvoyer le carré de la distance entre deux points;
- un test dans la fonction “arbre“: on n’exécute la fonction que si $AB^2 > 8$ (par exemple). En effet, inutile d’aller plus loin si l’on ne voit plus les points.
Cette modification donne: