\(\pi\) est la constante définie comme étant le rapport de la circonférence d’un cercle et de son diamètre. Et on arrive à démontrer que l’aire du disque défini par ce cercle est égale à : $$\mathcal{A}=\pi \times r^2.$$Nous allons voir dans cet article comme utiliser cette dernière égalité afin de trouver une valeur approchée de \(\pi\) en passant par les probabilités.

Approche théorique

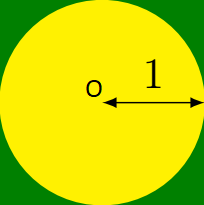
Considérons un disque (jaune) de centre O et de rayon 1 inscrit dans un carré (vert). Intuitivement, si l’on prend un point au hasard dans le carré vert, la probabilité pour qu’il soit dans le disque jaune est égale à la proportion de ce dernier dans le carré, à savoir :$$\frac{\text{aire du disque}}{\text{aire du carré}}=\frac{\pi \times 1^2}{2 \times 2}=\frac{\pi}{4}.$$

Ainsi, si l’on arrive à déterminer une valeur approchée de cette probabilité, on arrivera à trouver une valeur approchée de \(\pi\) en multipliant par 4. C’est l’objectif de la méthode de Monte-Carlo.

Méthode de Monte-Carlo

L’idée est de considérer l’expérience consistant à choir un point au hasard dans le carré vert et à regarder s’il est dans le disque jaune, puis de répéter cette expérience un assez grand nombre de fois afin de calculer la proportion de points à l’intérieur du disque par rapport au nombre total de points. Nous allons implémenter cela en Python.

On va imaginer une fonction is_in() renvoyant 1 si un point choisi au hasard est dans le cercle, et renvoyant 0 sinon. Pour cela, on se place dans un repère (O,I,J), où le disque jaune est de centre O. On choisit au hasard deux nombres a et b, tous deux compris entre 0 et 1 et on calcule les coordonnées d’un point M(x;y) tel que \( x = -1 + 2a \) et \(y = -1+ 2b\); ainsi, M est dans le carré vert.

Ensuite, on regarde si M est dans le disque jaune; pour cela, on calcule la distance OM:$$OM=\sqrt{x^2+y^2}.$$ Si cette distance est inférieure ou égale à 1, cela signifie que M est dans le disque; la fonction doit alors renvoyer « 1 »; sinon, elle renvoie 0.

Cela donne:

from random import random
def is_in():
    a = random() # choisit un nombre aléatoire entre 0 et 1
    b = random()
    x = -1 + 2 * a # absisse d'un point M comprise entre -1 et 1
    y = -1 + 2 * b # ordonnée de M comprise entre -1 et 1
    
    d = ( x**2 + y**2 )**0.5 # distance OM

    if d <= 1: # si M est dans le disque...
        return 1
    else:     # sinon...
        return 0

[Ajout du 14/06/2021 suite à un commentaire] Comme le rayon de notre disque est égal à 1, on peut aussi comparer le carré de la distance, ce qui permet de gagner en terme de complexité algorithmique, et donc gagner du temps :

from random import random
def is_in():
    a = random() # choisit un nombre aléatoire entre 0 et 1
    b = random()
    x = -1 + 2 * a # absisse d'un point M comprise entre -1 et 1
    y = -1 + 2 * b # ordonnée de M comprise entre -1 et 1
    
    d = x**2 + y**2  # carré de la distance OM

    if d <= 1: # si M est dans le disque...
        return 1
    else:     # sinon...
        return 0

Maintenant, nous devons simuler un grand nombre de fois cette expérience, disons 10 000 fois (par exemple).

N = 0 # nombre de points à l'intérieur du disque
f = 5000000

for n in range(f):
    N += is_in()

print("PI est à peu près égal à {}".format(4 * N / f))

Prendre 10 000 points peut paraître énorme, mais il n’en est rien… En effet, la valeur retournée est assez éloiognée de \(\pi\) (j’ai obtenu 3.14296). Bon, vous allez me dire, c’est pas si éloigné que ça crévindiou ! Mouais… M’enfin… Y’a mieux ! En prenant 10 000 000 points, on arrive à 3.1417784, et pour n = 100 000 000 (avec un peut de patience car il faut tout de même exécuter pas mal d’opérations et cela ne se fait pas en quelques secondes uniquement), j’obtiens 3.14124084… Pas sûr que ça vallait l’attente de plusieurs minutes…

Pourquoi cette méthode est aussi pourrie ?

En fait, ce n’est pas la méthode qui est nulle, mais les résultats trouvés par Python. Il ne faut pas oublier déjà que le hasard n’existe pas en informatique. Ainsi, la simulation du hasard n’est qu’un pseudo-hasard, ce qui peut expliquer en partie les résultats décevants que nous avons obtenus. De plus, les points pris aléatoirement peuvent être trop proches, voire confondus, ce qui fait qu’on peut compter deux fois un « même » point et on peut imaginer que tous les points pris aléatoirement « ne couvrent pas entièrement le disque » (oui, c’est assez abusif de dire ça, mais bon… j’essaie de simplifier). En effet, imaginez au pire des cas que tous les points choisis au hasard tombent au même endroit dans le disque : la probabilité obtenue sera alors égale à 1, soit une valeur approchée de \(\pi\) égale à 4… !

Alors bien sûr, l’algorithme de « random » est performant et il n’y a aucune chance qu’un grand nombre de points tombent presque au même endroit, mais cet algorithme ne reflète pas non plus la réalité…

Donc en théorie, la méthode de Monte-Carlo est intéressante, mais dans la pratique, elle ne vaut pas grand-chose…