Démonstration de la première égalité d’Euclide pas à pas après avoir vu bien entendu ce qu’était cette égalité.

L’énoncé

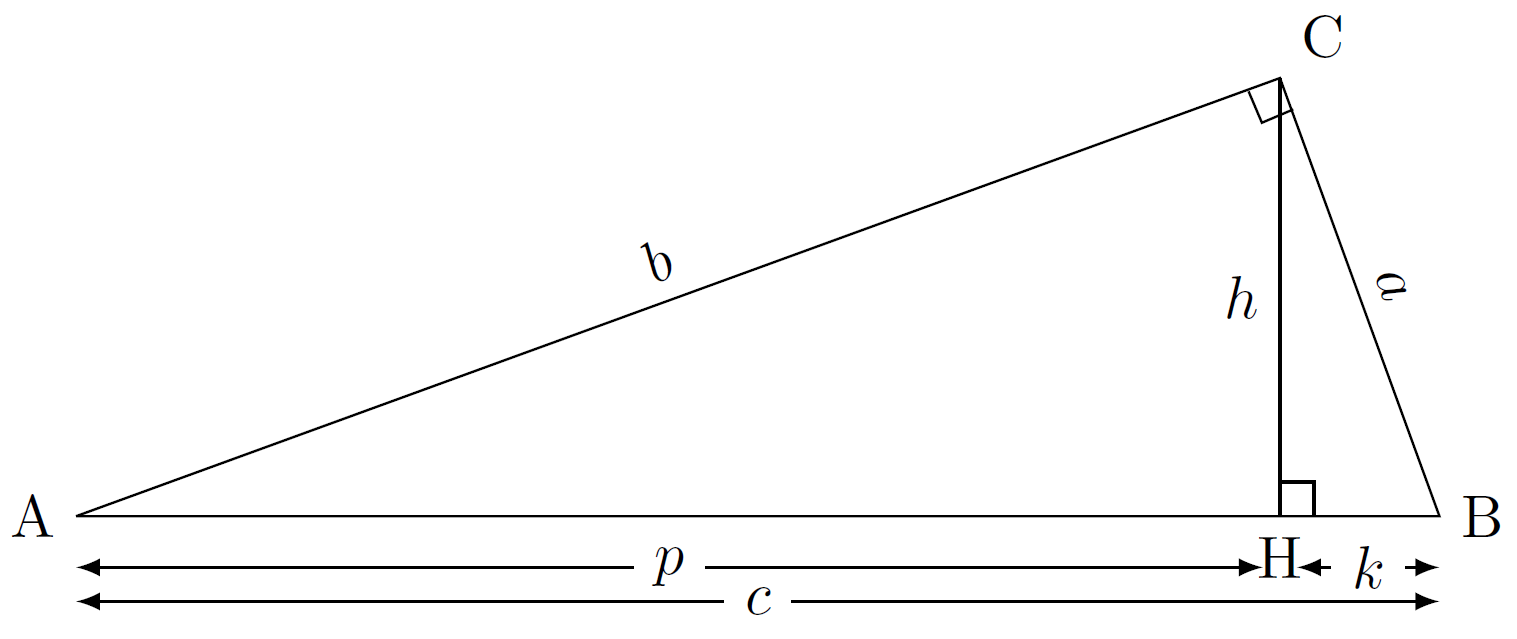
On considère un triangle ABC rectangle en C.

Soit H le pied de la hauteur de ce triangle issue du sommet C.

Si l’on convient d’utiliser les notations portées sur le dessin ci-dessus, alors:$$h^2=pk.$$

Démonstration de la première égalité d’Euclide: à l’aide du théorème de Pythagore

D’après le théorème de Pythagore appliqué dans le triangle ABC rectangle en C,$$c^2=a^2+b^2.$$On peut alors en conclure que:$$a^2=c^2-b^2$$et donc:$$a^2=(p+k)^2-b^2=p^2+k^2+2pk-b^2.$$

Le même théorème appliqué dans le triangle CHA rectangle en H,$$h^2=b^2-p^2.$$

Appliqué dans le triangle CHB rectangle en H, on a:$$h^2=a^2-k^2.$$

On en déduit alors:$$\begin{array}{rl} b^2-p^2 & = a^2-k^2\\b^2-p^2 & = p^2+k^2+2pk-b^2-k^2 \\ 2b^2 & = 2p^2 + 2pk\\ b^2 & = p^2 + pk\end{array}$$

Ainsi,$$h^2=b^2-p^2=p^2 + pk-p^2\quad\text{soit}\quad h^2=pk.$$

À quel niveau peut-on faire cette démonstration ?

Comme vous pouvez le constater, pour démontrer cette égalité d’Euclide, j’utilise l’égalité de Pythagore et la notion de transitivité. On peut donc envisager cette démonstration dès la classe de 4ème.

De plus, elle n’est pas très longue ni compliquée. En guidant les élèves avec quelques questions, elle permet à ces derniers d’acquérir de l’aisance en justification. La classe de 4ème est justement le bon moment pour assoir l’art de la démonstration.

Pour les abonné·e·s de ce site, voici le code source \(\LaTeX\) de la figure (en TiKZ).

\documentclass{standalone}
\usepackage{tikz}
\usetikzlibrary{calc}
\setlength{\parindent}{0pt}
\begin{document}
\begin{tikzpicture}
\draw (-4,0) node[left] {A} -- (4,0) node[right] {B} -- (40:4) node[midway,above,rotate=-70] {$a$} node[above right] {C} -- (-4,0) node[midway,above,rotate=30] {$b$};
\draw (40:4) -- ({4*cos(40)},0) node[below] {H} node[midway,left] {$h$};
\draw ({4*cos(40)},0.2) -- ({4*cos(40)+0.2},0.2) -- ({4*cos(40)+0.2},0);
\begin{scope}[shift=(40:4),rotate=-157]
\draw (0,0.2) -- (0.2,0.2) -- (0.2,0);
\end{scope}
\draw[<->,>=latex] (-4,-.3) -- ({4*cos(40)-.1},-.3) node[midway,fill=white] {$p$};
\draw[<->,>=latex] ({4*cos(40)+.1},-.3) -- (4,-.3) node[midway,fill=white] {$k$};
\draw[<->,>=latex] (-4,-.5) -- (4,-.5) node[midway,fill=white,inner ysep=0pt] {$c$};
\end{tikzpicture}
\end{document}