Planche de Galton, Python et LaTeX. Sur cette page, j’ai expliqué comment simuler l’expérience de la planche de Galton à l’aide de Python. Je souhaite dans cet article aller plus loin en obtenant un fichier PDF du résultat obtenu avec \(\LaTeX\).
Il y a deux approches possibles: utiliser PythonTeX, ou générer le fichier \(\LaTeX\) directement en Python.
Planche de Galton, Python et LaTeX : approche avec pythontex
C’est l’approche la moins intéressante. En effet, cette compilation a un inconvénient majeur: à chaque fois, il est nécessaire de supprimer les fichiers auxiliaires créés par la compilation pour obtenir un nouveau document. Je m’explique: je compile le document suivant via pythontex.
\documentclass{article}
\usepackage{tikz}
\usepackage{pythontex}
\usepackage[margin=5mm]{geometry}
\begin{document}
\begin{center}
\begin{pycode}
from random import choice
def simulation_galton(c = 7 , n = 20):
base = c * [0]
for bille in range(n):
position = c // 2
for clou in range(c-1):
position += choice([-1,1])/2
base[ int(position) ] += 1
return base
def graph_latex( L ):
ligne = '\\begin{tikzpicture}\n'
for i in range(len(L)): # pour chaque élément de L
if L[i] != 0: # si l'élément est non nul
for y in range(1,L[i]): # on trace L[i] billes à la verticale
ligne += '\\shade[ball color = blue] (' + str(i+0.5) + ' , ' + str(y) + ') circle (5mm);\n'
ligne += '\\draw[very thick] (0,0.5) -- (' + str(len(L)) + ',0.5);\n'
for x in range( len(L)+1 ):
ligne += '\\draw[very thick] ('+str(x)+','+str(0.5)+') -- ('+str(x)+','+str( max(L) )+');\n'
for y in range( len(L) ):
for x in range( y ):
ligne += '\\fill[gray] (' + str(1+3-y/2+x) + ',' + str(max(L) + 0.5 + 1.5*(len(L)-y-1)) + ') circle (1mm);\n'
ligne += '\\end{tikzpicture}'
return ligne
print( graph_latex( simulation_galton(n=50) ) )
\end{pycode}
\end{center}
\end{document}
et j’obtiens le PDF suivant:
Mais à ce stade, si je ne fais rien de plus que compiler à nouveau, j’obtiens exactement le même document. Or, ce que je voudrais, c’est une autre simulation… Pour se faire, je suis obligé de supprimer le répertoire pythontex-files-temp créé lors de la compilation via pythontex.
Ce n’est pas pratique… C’est pour cela que je préfère la seconde façon.
Approche avec génération du code \(\LaTeX\) en Python
Cette approche est à mon sens bien plus efficace.
On part du programme Python suivant:
from random import choice
from os import system
def simulation_galton(c = 7 , n = 20):
base = c * [0]
for bille in range(n):
position = c // 2
for clou in range(c-1):
position += choice([-1,1])/2
base[ int(position) ] += 1
return base
def graph_latex( L ):
ligne = '\\documentclass{standalone}\n'
ligne += '\\usepackage{tikz}\n'
ligne += '\\begin{document}\n'
ligne += '\\begin{tikzpicture}\n'
for i in range(len(L)): # pour chaque élément de L
if L[i] != 0: # si l'élément est non nul
for y in range(1,L[i]): # on trace L[i] billes à la verticale
ligne += '\\shade[ball color = blue] (' + str(i+0.5) + ' , ' + str(y) + ') circle (5mm);\n'
ligne += '\\draw[very thick] (0,0.5) -- (' + str(len(L)) + ',0.5);\n'
for x in range( len(L)+1 ):
ligne += '\\draw[very thick] ('+str(x)+','+str(0.5)+') -- ('+str(x)+','+str( max(L) )+');\n'
for y in range( len(L) ):
for x in range( y ):
ligne += '\\fill[gray] (' + str(1+3-y/2+x) + ',' + str(max(L) + 0.5 + 1.5*(len(L)-y-1)) + ') circle (1mm);\n'
ligne += '\\end{tikzpicture}\n'
ligne += '\\end{document}'
return ligne
"""
création du fichier LaTeX
"""
latex = graph_latex( simulation_galton(n=50) )
fichier = open('galton.tex' , 'w', encoding = 'utf8')
fichier.write( latex )
fichier.close()
"""
compilation via pdflatex
"""
system('pdflatex galton.tex')
system('start galton.pdf')
Il va d’une part simuler une expérience (ici, avec 7 colonnes et 50 billes), générer le fichier \(\LaTeX\), le compiler et afficher le PDF, comme celui-ci par exemple:
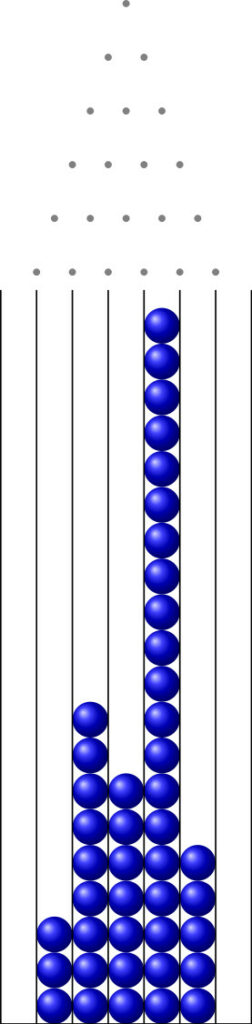
Il est alors aisé de modifier légèrement le programme Python pour générer autant d’expériences que souhaité.
"""
création des fichiers LaTeX & PDF
"""
ext = [ 'log' , 'tex' , 'aux' ]
for k in range(5):
latex = graph_latex( simulation_galton(n=50) )
fichier = open('galton-'+str(k+1)+'.tex' , 'w', encoding = 'utf8')
fichier.write( latex )
fichier.close()
"""
compilation via pdflatex
"""
system('pdflatex galton-'+str(k+1)+'.tex')
for e in ext:
system('erase galton-' + str(k+1) + '.' + e)
Ici, j’ai opté pour le fait de supprimer tous les fichiers qui ne servent à rien pour ne garder que les fichiers PDF.
À noter que je suis sous Windows 10; j’utilise donc la commande “erase”. Sous Linux et MacOS, il me semble que c’est la commande “rm <fichier.ext>”.
La simulation de ces expériences est au programme de spécialité mathématiques en Terminale. Cette dernière approche peut donc aider les enseignant·e·s à construire un cours avec illustrations.


