Le théorème de Pick

  • Dernière modification de la publication :26 octobre 2021
  • Temps de lecture :12 min de lecture

Loading

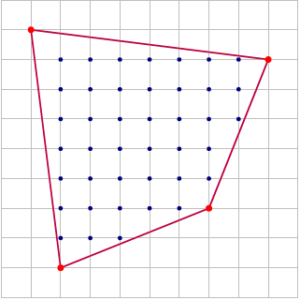
On considère un polygone convexe, c’est-à-dire une figure géométrique constituée de plusieurs côtés rectilignes de sorte qu’aucun sommet ne « rentre »  dans la figure, sur un maillage régulier de sorte que chaque sommet soit sur un nœud de ce maillage comme l’illustre le schéma ci-dessous.

Le théorème de Pick stipule que la superficie du polygone peut être calculée de façon simple à l’aide de la formule :  \[ \mathcal{A}=i+\frac{b}{2}-1\]
exprimée en unités d’aire, où « i » représente le nombre de nœuds intérieurs au polygone et « b » celui des nœuds se trouvant sur ses côtés.

(suite…)

Continuer la lectureLe théorème de Pick
théorème de Viviani

Le théorème de Viviani

  • Dernière modification de la publication :26 octobre 2021
  • Temps de lecture :7 min de lecture

Loading

Le théorème de Viviani stipule que : « dans un triangle équilatéral, la somme des distances d’un point intérieur quelconque aux trois côtés est constante. »

théorème de Viviani

Autrement dit, quelle que soit la position du point M dans le triangle ABC, \[ \text{MS}+\text{MQ}+\text{MO} = \text{constante}.\]

(suite…)

Continuer la lectureLe théorème de Viviani
méthode de Hörner

La méthode de Hörner

  • Dernière modification de la publication :30 décembre 2023
  • Temps de lecture :8 min de lecture

Loading

La méthode de Hörner va nous permettre de trouver les coefficients du polynôme Q tel que : \[P(x)=(x-a)Q(x)\] où P est un polynôme dont une racine est égale à a.

Bien entendu, il existe d’autres méthodes, comme la division euclidienne de polynômes ou encore la méthode des coefficients indéterminés, mais nous allons voir que la méthode de Hörner a deux avantages sur les autres : sa rapidité et le fait que l’on puisse la programmer aisément.

méthode de Hörner
(suite…)

Continuer la lectureLa méthode de Hörner

Les différentes moyennes

  • Dernière modification de la publication :26 octobre 2021
  • Temps de lecture :13 min de lecture

Loading

EDF souhaite augmenter ses tarifs de 30 % sur 5 ans, soit une augmentation moyenne de 6 % par an.

C’est à peu près ce que j’ai pu entendre il y a quelques années sur beaucoup de chaînes de télévision de la part de certains journalistes. Et cela m’a un peu fait mal aux oreilles car ce n’est pas correct, et pour s’en rendre compte, il est nécessaire de revenir sur la notion de moyenne…

(suite…)

Continuer la lectureLes différentes moyennes

L’existence de Pi

  • Dernière modification de la publication :26 octobre 2021
  • Temps de lecture :6 min de lecture

Loading

À l’école primaire, les élèves prennent connaissance de l’existence d’un nombre mystérieux nommé « Pi » et noté par la lettre grecque « \(\pi\) » par Archimède, en rapport avec l’initiale du mot  « \(\pi\varepsilon\rho\iota\mu\varepsilon\tau\rho o\zeta\) » (« périmètre » en français).

À ce stade de l’apprentissage, les professeurs des écoles disent que la valeur de Pi est 3,14 et j’espère qu’ils ajoutent que ce n’est qu’une valeur approchée de ce nombre qui admet une partie décimale infinie. D’ailleurs, tout nombre qui ne peut pas s’écrire entièrement est désigné par une lettre ou autre chose de « rapide à écrire » et c’est la raison pour laquelle Pi est désigné par une lettre : on ne peut pas l’écrire en entier.

On définit le nombre \(\pi\) comme étant le rapport constant entre le périmètre d’un cercle et son diamètre (il faut entendre ici : dans le plan euclidien). Mais pourquoi ce rapport est-il constant ? Comment a-t-on pu démontrer que \(\pi\) existait ? Nous allons le voir ici …

(suite…)

Continuer la lectureL’existence de Pi
equation degré 3

Équations polynomiales de degré 3

  • Dernière modification de la publication :18 juin 2022
  • Temps de lecture :11 min de lecture

Loading

Les équations polynomiales de degré 3 sont de la forme : \[  ax^3+bx^2+cx+d=0.\qquad(1) \]

Ce dont nous pouvons être assuré.e.s, c’est qu’elle admet au moins une solution réelle. En effet, la fonction : \[ f(x)=ax^3+bx^2+cx+d\]

est continue sur \(\mathbb{R}\) et, de plus, \[ \left\{ \begin{array}{l} \lim\limits_{x\to-\infty} f(x)=\lim\limits_{x\to-\infty} (ax^3)=\text{sgn}(-a)\infty\\\lim\limits_{x\to+\infty} f(x)=\lim\limits_{x\to+\infty} (ax^3)=\text{sgn}(a)\infty\end{array}\right.\]

où \(\text{sgn}(a)\) désigne le signe de a.

Ainsi, d’après le théorème des valeurs intermédiaires, l’équation \(f(x)=0\) admet au moins une solution sur \(\mathbb{R}\).

(suite…)

Continuer la lectureÉquations polynomiales de degré 3

Circonscrire un polygone : la constante de Kasner-Newman

  • Dernière modification de la publication :4 février 2021
  • Temps de lecture :8 min de lecture

Loading

Dans les années 1940, les mathématiciens Edward Kasner et James Roy Newman découvrirent une constante :
\[ R=\frac{1}{\cos\left(\frac{\pi}{3}\right)\times\cos\left(\frac{\pi}{4}\right)\times\cos\left(\frac{\pi}{5}\right)\times\cdots} \]
que l’on peut aussi écrire : \[ R=\prod_{n\geq3}\frac{1}{\cos\left(\frac{\pi}{n}\right)}.\]

Ils découvrirent cette constante de la manière suivante : on construit successivement :

  1. un cercle de rayon r;
  2. le triangle équilatéral circonscrit à ce cercle;
  3. le cercle circonscrit au triangle équilatéral;
  4. le carré circonscrit au dernier cercle;
  5. le cercle circonscrit au carré;
  6. le pentagone régulier circonscrit au dernier cercle;
  7. le cercle circonscrit au pentagone;
  8. l’hexagone circonscrit au dernier cercle;
  9. etc.

En observant le rayon des cercles, on s’aperçoit que l’on se rapproche de plus en plus d’une valeur proportionnelle à R (définie précédemment).

(suite…)

Continuer la lectureCirconscrire un polygone : la constante de Kasner-Newman

Créer des animations GIF avec Geogebra : mission impossible ?

  • Dernière modification de la publication :13 septembre 2018
  • Temps de lecture :3 min de lecture

Loading

Geogebra n’est plus à présenter. Ce logiciel de géométrie (entre autre) permet quelque fois de présenter en cours des choses plutôt sympas.

Dans cet article, je vais prendre pour prétexte une activité que j’avais proposée à mes élèves de 6ème afin de créer une animation et au final, un Gif.

(suite…)

Continuer la lectureCréer des animations GIF avec Geogebra : mission impossible ?