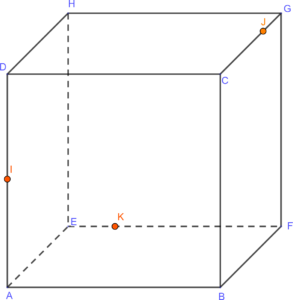
Nous allons voir dans cet article comment trouver la section d’un cube par un plan quand on connaît 3 points sur 3 arêtes de ce cube, chacun des points n’étant pas sur une face où se trouve l’un des deux autres.
Étape 1 : on projette orthogonalement un point sur l’arête parallèle à celle où il se trouve et contenue dans une face où se trouve l’un des deux autres points.
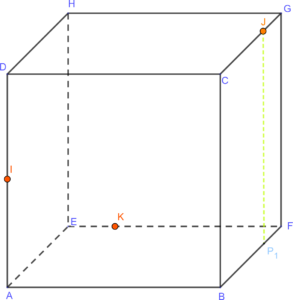
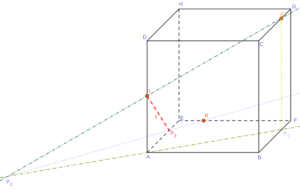
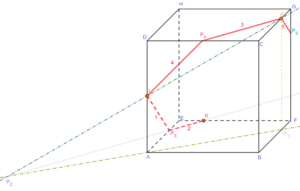
Ici, on va projeter le point J sur [BF] car [BF] est contenue dans une face où se trouve K. On obtient un point que l’on nomme \(P_1\).
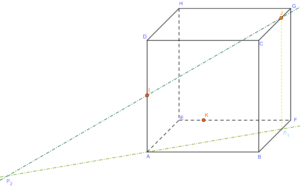
Étape 2 : on trace un triangle passant par le sommet opposé à la face contenant le point choisi et son projeté.
Ici, on trace \((AP_1)\) et \((IJ)\). Elles sont coplanaires et non parallèles donc se coupent en un point \(P_2\).
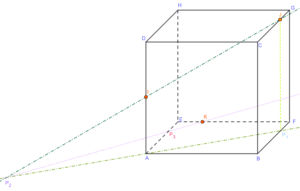
Étape 4 : on trouve enfin un point qui appartient à la section cherchée.
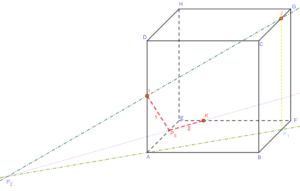
Les points K et \(P_2\) appartiennent à la même face (ABFE) donc la droite \((KP_2)\) coupe l’arête [AE] (car elles ne sont pas parallèles). On obtient alors le point \(P_3\).
On a ainsi l’intersection des plans (IJK) et (ADHE):
ainsi que celle des plans (IJK) et (ABFE):
Étape 5 : on trace des parallèles
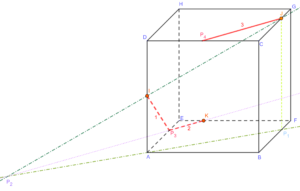
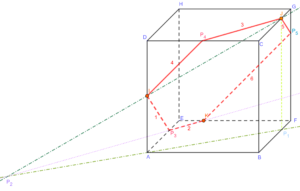
On trace maintenant la droite parallèle à \((KP_3)\) passant par J : elle coupe l’arête [DC] en \(P_4\):
On trace ensuite \([IP_4]\) qui est un autre côté de la section cherchée:
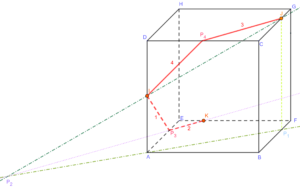
Puis la parallèle à \((IP_3)\) passant par J, qui coupe [GF] en \(P_5\):
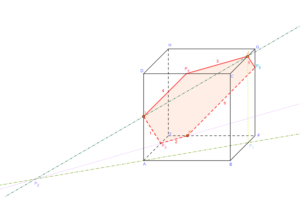
On trace enfin \([KP_5]\) qui ferme la section cherchée:
La section du cube par le plan (IJK) est le polygone \(KP_5JP_4IP_3\):
Bonjour. Merci pour cette explication très claire.
Je reviens vers vous pour proposer une correction dans l’étape 2.
Ici, on trace (AP1) et (IJ) et non (AP1) et (AJ). En outre il faut préciser qu’elles sont concourantes parce que coplanaires.
Erreur de frappe bien sûr. Pour ce qui est de la justification, je ne l’avais pas mise car évidente et ce n’est pas non plus un cours… juste un article lu essentiellement par des enseignants. Mais, sait-on jamais, je l’ai ajoutée. Ça ne fait pas de mal…
top