À l’école primaire, les élèves prennent connaissance de l’existence d’un nombre mystérieux nommé « Pi » et noté par la lettre grecque « \(\pi\) » par Archimède, en rapport avec l’initiale du mot  « \(\pi\varepsilon\rho\iota\mu\varepsilon\tau\rho o\zeta\) » (« périmètre » en français).

À ce stade de l’apprentissage, les professeurs des écoles disent que la valeur de Pi est 3,14 et j’espère qu’ils ajoutent que ce n’est qu’une valeur approchée de ce nombre qui admet une partie décimale infinie. D’ailleurs, tout nombre qui ne peut pas s’écrire entièrement est désigné par une lettre ou autre chose de « rapide à écrire » et c’est la raison pour laquelle Pi est désigné par une lettre : on ne peut pas l’écrire en entier.

On définit le nombre \(\pi\) comme étant le rapport constant entre le périmètre d’un cercle et son diamètre (il faut entendre ici : dans le plan euclidien). Mais pourquoi ce rapport est-il constant ? Comment a-t-on pu démontrer que \(\pi\) existait ? Nous allons le voir ici …

Démonstration de l’existence de Pi

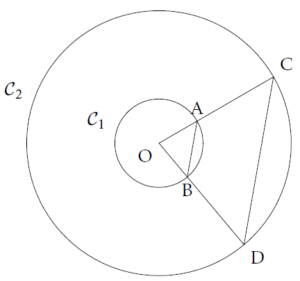
Considérons deux cercles concentriques \(\mathcal{C}_1\), de rayon \(r_1\), et \(\mathcal{C}_2\), de rayon \(r_2\), avec \(r_1<r_2\). On appelle O le centre de ces cercles.

On trace deux rayons [OC] et [OD] de \(\mathcal{C}_2\) et on note A et B les points d’intersection respectifs de [OC] et [OD] avec \(\mathcal{C}_1\).

Par construction, \[ \frac{\text{OA}}{\text{OC}}=\frac{\text{OB}}{\text{OD}}=\frac{r_1}{r_2} \]

et donc, d’après la réciproque du théorème de Thalès, \[ (\text{AB})~//~(\text{CD}).\]

On peut ainsi conclure, d’après le théorème de Thalès,  que :  \[ \frac{r_1}{r_2}=\frac{\text{AB}}{\text{CD}}.\]

Par conséquent, les produits en croix sont égaux : \[ r_1\times\text{CD}=r_2\times\text{AB}\]

et donc, en divisant par \(\text{AB}\times\text{CD}\) : \[ \frac{r_1}{\text{AB}}=\frac{r_2}{\text{CD}}.\qquad(1) \]

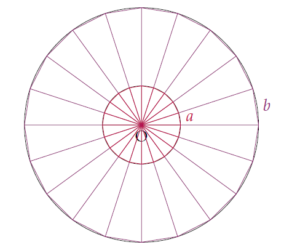
Construisons maintenant n triangles identiques comme l’illustre le schéma suivant :

Tous les triangles sont identiques, inscrits dans les cercles et isocèles en O.

Les triangles inscrits dans \(\mathcal{C}_1\) ont pour base a et ceux inscrits dans \(\mathcal{C}_2\) ont pour base b.

L’égalité (1) nous dit que : \[  \frac{r_1}{n\times a}=\frac{r_2}{n\times b}.\qquad (2) \]

Si on augmente le nombre de triangles, c’est-à-dire si l’on fait tendre n vers l’infini, alors \(n\times a\) se rapproche du périmètre de \(\mathcal{C}_1\) (que l’on va noter \(\mathcal{P}_1\)) et \(n\times b\) vers le périmètre de \(\mathcal{C}_2\) (que l’on va noter \(\mathcal{P}_2\)).

Ainsi, l’égalité (2) devient, par passage à la limite : \[ \frac{r_1}{\mathcal{P}_1}=\frac{r_2}{\mathcal{P}_2}, \]

ou, si l’on préfère : \[ \frac{\mathcal{P}_1}{r_1}=\frac{\mathcal{P}_2}{r_2}.\]

En multipliant cette dernière égalité par \(\displaystyle\frac{1}{2}\), on obtient : \[ \frac{\mathcal{P}_1}{2r_1}=\frac{\mathcal{P}_2}{2r_2} ,\]

soit : \[ \frac{\mathcal{P}_1}{D_1}=\frac{\mathcal{P}_2}{D_2},\]

c’est-à-dire que, quel que soit le rayon du cercle que l’on prend, le rapport entre son périmètre et son diamètre est constant.

C’est ce rapport que l’on a décidé de noter \(\pi\).

Les sources \(\LaTeX\) du document PDF :