EDF souhaite augmenter ses tarifs de 30 % sur 5 ans, soit une augmentation moyenne de 6 % par an.
C’est à peu près ce que j’ai pu entendre il y a quelques années sur beaucoup de chaînes de télévision de la part de certains journalistes. Et cela m’a un peu fait mal aux oreilles car ce n’est pas correct, et pour s’en rendre compte, il est nécessaire de revenir sur la notion de moyenne…
Reprenons l’exemple d’EDF ; nous avons alors le schéma suivant, où t est le pourcentage d’augmentation moyen annuel et \(x_0\) le prix initial :
D’après ce schéma, \(x_1=\left(1+\frac{t}{100}\right)x_0\) et par suite, \(x_5=\left(1+\frac{t}{100}\right)^5x_0\).
On souhaite une augmentation globale de 30 % ; ainsi, \(\left(1+\frac{t}{100}\right)^5=1+\frac{30}{100}\). On résout cette équation de la façon suivante :
\[ \begin{array}{ll} \left(1+\frac{t}{100}\right)^5=1,3 & \Longleftrightarrow \ln\left(1+\frac{t}{100}\right)^5=\ln 1,3\\ & \Longleftrightarrow 5\ln\left(1+\frac{t}{100}\right)=\ln 1,3\\ & \Longleftrightarrow \ln\left(1+\frac{t}{100}\right)=\frac{\ln 1,3}{5}\\ & \Longleftrightarrow \exp\left[\ln\left(1+\frac{t}{100}\right)\right]=\exp\left(\frac{\ln 1,3}{5}\right)\\ & \Longleftrightarrow 1+\frac{t}{100}=\exp\left(\frac{\ln 1,3}{5}\right)\\ & \Longleftrightarrow \frac{t}{100}=\exp\left(\frac{\ln 1,3}{5}\right)-1\\ & \Longleftrightarrow t=100\left[\exp\left(\frac{\ln 1,3}{5}\right)-1 \right]\\ & \Longleftrightarrow t \approx 5,3874 \end{array} \]
On voit donc ici que l’on n’obtient pas le même taux d’augmentation… Si l’on avait appliqué une augmentation de 6 % par an, alors l’augmentation globale aurait été bien supérieure à celle annoncée ! Espérons qu’EDF ne fasse pas les mêmes erreurs de calculs que les journalistes…
Le concept de moyenne échappe à bon nombre de personnes; il est donc important de préciser qu’il n’existe pas qu’une seule moyenne. Ce concept a été notamment étudié par l’école pythagoricienne.
La moyenne arithmétique
C’est la moyenne la plus connue, et pour cause : on l’utilise dès l’enseignement primaire.
On l’utilise quand on a des grandeurs absolues, c’est-à-dire quand les unités sont simples (contrairement aux grandeurs produits ou quotients, comme les vitesses, ou aux grandeurs relatives, comme les pourcentages).
Exemple
On parle de moyenne arithmétique quand on souhaite calculer le prix moyen que l’on a dépensé en faisant nos courses. Ce prix moyen correspond à un nombre qui, multiplié par le nombre d’articles, est égal au montant total que l’on a payé.
J’ai ici répertorié les différents prix des articles que j’ai acheté récemment : \[ 0,96 ~;~ 2,02 ~;~ 0,49 ~;~ 0,39 ~;~ 0,63 ~;~ 4,08 ~;~ 1,59 ~;~ 3,15 ~;~ 1,26 ~;~ 1,08 ~;~ 2,70 ~;~ 1,10.\]
Le montant total est de 19,45 € pour 12 articles.
Ainsi, le prix moyen d’un article est : \[ m=\frac{19,45}{12}\approx 1,62083.\]
Ce nombre correspond au fait que, si on le multiplie par le nombre total d’articles, on trouve la dépense totale. On a ainsi la formule suivante : \[ m=\frac{x_1+x_2+x_3+\cdots+x_{n-2}+x_{n-1}+x_n}{n} \]
où \(x_1,\ x_2,\ \cdots, x_n\) représentent les valeurs dont on veut trouver la moyenne arithmétique.
La moyenne arithmétique pondérée
C’est la moyenne qui est la plus connue après la moyenne arithmétique (simple). Le principe est le même que précédemment si ce n’est que chaque valeur a un « poids », c’est-à-dire une importance, qui lui est propre.
Exemple 1 : moyenne trimestrielle d’un élève.
Un élève a obtenu trois notes lors d’un trimestre : 14/20 (coef. 3), 15/20 (coef. 2) et 19/20 (coef. 1).
Avoir une note avec un coefficient 3 signifie qu’elle va compter 3 fois. Ainsi, c’est comme si on devait calculer la moyenne des nombres 14, 14, 14, 15, 15 et 19. On peut donc se ramener à la moyenne arithmétique (simple) ou bien affecter à chacune des notes leur coefficient (en les multipliant par leur coefficient), puis en divisant par le nombre de notes totales (donc ici, la somme des coefficients). D’où le calcul : \[ m_p=\frac{14\times 3+15\times 2+19\times 1}{3+2+1}=\frac{91}{6}\approx 15,17. \]
En définitive, la formule qui permet de calculer la moyenne pondérée des valeurs \(\left(x_1~;~p_1\right)\), \(\left(x_2~;~p_2\right)\), …, \(\left(x_n~;~p_n\right)\), où les \(x_i\) sont les valeurs dont on veut trouver la moyenne et les \(p_i\) leur coefficient respectif, est : \[ m_p=\frac{x_1p_1+x_2p_2+\cdots+x_np_n}{p_1+p_2+\cdots+p_n} \]
Exemple 2 : barycentre de points pondérés.
Notre système solaire est constitué de plusieurs planètes et autres objets qui tournent autour d’un point… Ce point, c’est le centre de gravité du système solaire.
Ce point peut être situé grâce à une moyenne pondérée (en fait, plusieurs moyennes pondérées, une par coordonnée spatiale). On pense que c’est le Soleil, mais que nenni… Il se trouve que le centre de gravité se trouve très proche du Soleil mais n’est pas au centre du Soleil.
La moyenne géométrique
Nous abordons maintenant une notion presque étrangère au plus commun des mortels… Pourtant, elle ne devrait pas l’être puisque concernant des choses que l’on manipule assez souvent : les pourcentages.
Imaginons une suite de valeurs obtenues de la manière dont l’illustre le schéma suivant :
On souhaite trouver la valeur de t telle que \(x_i=tx_{i-1}\) pour i allant de 1 à n.
On sait alors que \(x_n=t_1\times t_2\times t_3\times\cdots\times t_n x_0=t^n x_0\), d’où la formule suivante : \[ t=\sqrt[n]{t_1t_2t_3\cdots t_{n-1} t_n} \]
Exemple
Un article subit une hausse de 13 %, puis une hausse de 10 %, puis une hausse de 15 %.
La hausse moyenne sera donc ici : \[ g=\sqrt[3]{1,13\times 1,10\times 1,15}\approx 1,1265,\]
soit une hausse moyenne de 12,65 %.
La moyenne harmonique
On se sert de cette moyenne notamment pour les grandeurs quotients, comme les vitesses par exemple.
Exemple
Un cycliste a une vitesse de 10 km/h sur une montée de colline, et 30 km/h sur la descente (même longueur).
Chacun des flancs a une longueur de 10 kilomètres.
Alors, le second flanc sera parcouru en 20 minutes (car il parcourt 30 km en 1 heure, donc 10 km seront parcourus en un tiers d’heure, soit un tiers de 60 minutes, c’est-à-dire 20 minutes). Quant au premier, il sera parcouru en 1 heure.
Ainsi, la vitesse moyenne du parcours total est : \[ v=\frac{10+10}{\frac{4}{3}}=\frac{60}{4}=15~\text{km}\cdot\text{h}^{-1}. \]
Si on effectue la moyenne arithmétique des vitesses, on obtient : \[ v^\prime=\frac{10+30}{2}=20~\text{km}\cdot\text{h}^{-1}. \]
Ainsi, la vitesse moyenne du parcours n’est pas la moyenne arithmétique des vitesses…
Si on calcule la moyenne arithmétique des inverses des vitesses, on a : \[ \frac{\frac{1}{10}+\frac{1}{30}}{2}=\frac{\frac{40}{300}}{2}=\frac{20}{300}=\frac{2}{30}.\]
On remarque alors que l’inverse du résultat est égal à \(\frac{30}{2}=15\), c’est-à-dire la vitesse moyenne obtenue précédemment.
Dans un cas général, en effet, la moyenne de deux vitesses est l’inverse de la moyenne arithmétique des inverses des vitesses. Autrement dit :
\[ \frac{2}{v}=\frac{1}{v_1}+\frac{1}{v_2}\]
On dit ici que v est la moyenne harmonique des valeurs \(v_1\) et \(v_2\).
Dans un cas plus général, la moyenne harmonique de n valeurs \(x_1,\ x_2,\cdots,\ x_n\) est la valeur h telle que : \[ \frac{n}{h}=\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}\]
Cette moyenne a été inventée par le disciple de Pythagore nommé Hippase de Métaponte. L’école pythagoricienne était réputée pour ses diverses études, notamment en musique.
« La moyenne harmonique fut ainsi dénommée car utilisée en musique afin d’obtenir des longueurs de cordes vibrantes produisant des accords harmonieux : il s’agit de la moyenne arithmétique des inverses, c’est-à-dire musicalement de la moyenne arithmétique des fréquences, inverses de la période. Rappelons ici que la fréquence fondamentale du son émis est inversement proportionnelle à la longueur de la corde. » (explication trouvée sur cette page).
La moyenne quadratique
Cette moyenne n’est pas beaucoup utilisée… On s’en sert principalement en statistiques pour évaluer l’écart-type, mais on peut la rencontrer en géométrie (voir exemple).
La moyenne quadratique des valeurs \(x_1,\ x_2,\cdots,\ x_n\) est : \[ q=\sqrt{\frac{x_1^2+x_2^2+\cdots+x_n^2}{n}}\]
Exemple
Soient un rectangle \(\mathfrak{R}\), de longueur L et de largeur \(\ell\), et un carré \(\mathfrak{C}\), de côté c. On cherche à calculer c de sorte à ce que les diagonales de \(\mathfrak{C}\) aient la même longueur que celles de \(\mathfrak{R}\).
D’après le théorème de Pythagore, une diagonale de \(\mathfrak{C}\) a pour longueur \(d_\mathfrak{C}~=~c\sqrt{2}.\)
D’après le même théorème, une diagonale de \(\mathfrak{R}\) a pour longueur \(d_\mathfrak{R}~=~\sqrt{L^2+\ell^2}\).
Ainsi, pour que les deux mesures soient égales, il faut que : \[ c=\frac{\sqrt{L^2+\ell^2}}{\sqrt{2}},\] c’est-à-dire : \[ c=\sqrt{\frac{L^2+\ell^2}{2}}.\]
On reconnaît ici la moyenne quadratique de L et \(\ell\).
Les sources \(\LaTeX\) du document PDF :
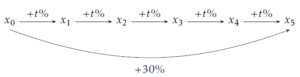
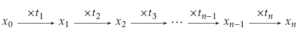



Bonjour dans une situation ou je n’ai que deux valeurs ou 3 y a t il une autre moyenne que l’arithmétique plus appropriée ?
La moyenne n’est pas une question de quantité de valeurs mais de contexte. Même si on a 1000 valeurs, il faut voir ce qu’elles représentent pour savoir quelle moyenne calculer.
Merci d’avoir présenter ce cours rapide. Seulement, l’exemple de EDF laisse à méditer pour intéressés non installés au pays de l’Hexagone…
Intéressant. Je cherchais à comprendre les formules des cordes en relation avec les différents type de moyenne… mais autant la 1ere CQ est facile à trouver (diagonale du carré de côté le rayon du cercle)… pour les autres ?
https://commons.wikimedia.org/wiki/File:MeansAsChords.svg?uselang=fr
Peut-être arriverez vous à trouver et expliquer ;o)
Cdlt.