On peut être matheux et romantique. La preuve : toutes ces équations de cœurs… Tiens ! C’est un bon prétexte pour parler de courbes paramétrées !

Pré-requis : courbes paramétrées

Dans le cursus scolaire français, nous voyons assez tôt, et longtemps, que certains phénomènes peuvent se traduire par des courbes, engendrées par des équations cartésiennes, c’est-à-dire des équations de la forme \(y=f(x)\) pour les plus simples.

Mais il existe d’autres types de courbes comme par exemple les courbes paramétrées (engendrées par des équations paramétriques) ou les courbes polaires.

• Les équations paramétriques de courbes planes sont de la forme : \[ \left\{\begin{array}{l}x=f(t)\\y=g(t)\end{array}\right.\] où f et g sont deux fonctions cartésiennes, et où (x ; y) représentent les coordonnées des points de la courbe paramétrée.
• Les équations polaires de courbes planes sont de la forme : \[\rho = f(\theta)\] où \(\rho\) représente la distance de l’origine O du repère \(O;\vec{i},\vec{j})\) au point M de la courbe, et \(\theta\) l’angle \(\Big(\widehat{\vec{i};\vec{OM}}\Big)\).

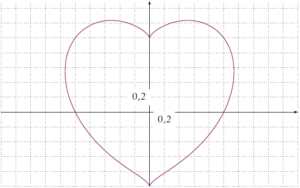
Le cœur d’Eugène Beutel (1909)

Ce cœur a pour équation cartésienne : \[(x^2+y^2-1)^3=x^2y^3.\]

Pour construire cette courbe, nous partons de l’équation d’origine et nous prenons la racine cubique de chaque membre : \[x^2+y^2-1=yx^{2/3}\] puis nous mettons tout dans le membre de gauche : \[ y^2-x^{2/3}y+x^2-1=0.\qquad (E) \]

Nous reconnaissons alors une équation polynomiale d’inconnue y de degré 2 et de discriminant : \[ \Delta=x^{4/3}+4-4x^2.\]

\(\Delta\geq0\) pour \(x\in[0;1,13902816469]\) (pour obtenir cela, on trace la courbe de la fonction f définie par \(f(x)=x^{4/3}+4-4x^2\), on remarque qu’elle est au-dessus de l’axe des abscisses de 0 à une certaine valeur de x, puis en-dessous. On résout alors à l’aide d’un logiciel de calculs formels l’équation \(x^{4/3}+4-4x^2=0\), et nous obtenons la valeur 1,13902816469).

Ainsi, nous obtenons deux solutions pour l’équation (E) : \[ y=\frac{x^{2/3}\pm\sqrt{x^{4/3}+4-4x^2}}{2}.\]

En traçant les courbes d’équations respectives : \[ y=\frac{x^{2/3}-\sqrt{x^{4/3}+4-4x^2}}{2}\] et \[ y=\frac{x^{2/3}+\sqrt{x^{4/3}+4-4x^2}}{2}\] sur [0 ; 1,139], nous obtenons la partie droite du cœur de Beutel.

Par symétrie par rapport à l’axe des ordonnées, nous obtenons l’autre partie, et ainsi le cœur en entier.

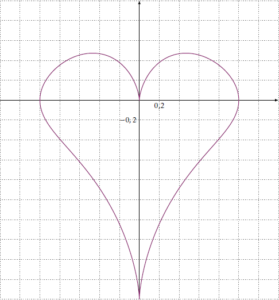
Le cœur de Raphaël Laporte (1993)

L’équation de cette courbe fut trouvée par Raphaël Laporte alors qu’il avait 16 ans, et ce pour sa petite amie… Là, si c’est pas romantique, je ne sais pas ce qui l’est !

Cette équation paramétrique est : \[\left\{\begin{array}{l}x=\sin^3t\\y=\cos t-\cos^4t\end{array}\right.\]

Il faut tout de même rappeler qu’en 1993, les courbes paramétrées étaient encore au programme de Terminale scientifique… ce qui n’est plus le cas en France depuis très (trop ?) longtemps.

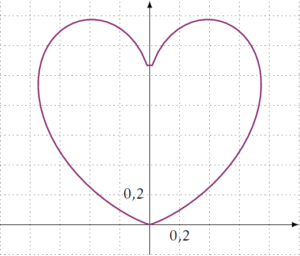
Le cœur de Dwight Boddorf (2008)

Ce cœur est donné par l’équation polaire suivante : \[\rho = \vert \tan\theta \vert^{\vert\cot\theta\vert}\quad,\quad0\leq\theta\leq\pi\]

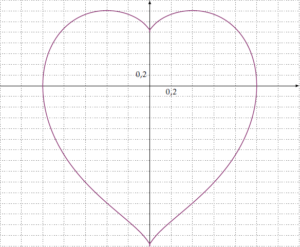
Le cœur  de Pierre Daniel (2013)

L’équation paramétrique de ce cœur est : \[\left\{\begin{array}{l}x^2=\frac{(1-t^2)^3}{1+t^2}\\y=\frac{4t}{1+t^2}-t^2\end{array}\right.\]

Pour en voir davantage :

• http://www.mathcurve.com/courbes2d/ornementales/ornementales.shtml
• http://www.mathematische-basteleien.de/heart.htm
• http://mathworld.wolfram.com/HeartCurve.html

Pour obtenir les sources \(\LaTeX\) du document PDF: