Introduction

La réforme du lycée s’accompagne de son lot de nouveautés. En mathématiques, des bruits courent sur la réapparition des équations différentielles dans le programme de la classe de maturité (Terminale).

Ceci me donne l’occasion de faire une brève (?) introduction de cette notion.

Définition

Dans équation différentielle, il y a d’abord « équation ». Par conséquent, il va y avoir au moins une inconnue (il n’y en a qu’une seule pour commencer). Cette inconnue, c’est une fonction. Elle est souvent désignée par la lettre y.

Ensuite, il y a le mot « différentielle », ce qui signifie que notre fonction inconnue va apparaître sous diverses formes dans notre équation en termes de différentiation, ce qui veut dire qu’il peut y avoir la fonction elle-même (y), mais aussi sa dérivée (y’) ainsi que sa dérivée seconde (y »), etc. Au lycée, on s’arrête à la dérivée seconde.

Si y » apparaît dans l’équation, on dira que l’on a affaire à une équation différentielle d’ordre 2.

Si tel n’est pas le cas mais que y’ apparaît, on dire que l’équation est d’ordre 1.

Les coefficients de y, y’ et y » sont au lycée des constantes, mais ils peuvent aussi être des fonctions.

De plus, les équations différentielles seront linéaires, c’est-à-dire qu’il n’y aura pas d’exposant aux inconnues (donc, par exemple, pas de y²).

Exemples d’équations différentielles linéaires

• y’ + 3y = x² est une équation différentielle d’ordre 1 à coefficients constants. Résoudre cette équation revient à trouver toutes les fonctions y telles que y’(x)+3y(x)=x² pour tout réel x.
• y » + 3y‘ – 5y = 0 est une équation différentielle d’ordre 2 à coefficients constants.
• (x+1)y » – x²y = x² + x + 1 est une équation différentielle d’ordre 2 à coefficients non constants.

Résolution de y‘ = ay

Nous allons avant tout nous pencher sur cette équation, qui est la plus simple (ou presque).

Il ne faut jamais oublier que y représente une fonction (ce que l’on oublie assez souvent au début car nous avions affaire jusqu’à présent qu’à des équations dont les inconnues étaient des nombres).$$\begin{align}y’=ay & \iff \frac{y’}{y}=a\\ & \iff \int_{\mathbb{R}}\frac{y’}{y}\text{d}x=\int_{\mathbb{R}} a\text{d}x\\&\iff \ln\big|y(x)\big|=ax+k,\ k\in\mathbb{R}\\&\iff y(x)=\text{e}^{ax+k}=\text{e}^k\times\text{e}^{ax}\\&\iff y(x)=C\text{e}^{ax},\ c\in\mathbb{R}.\end{align}$$

Précisions : à la deuxième ligne, on cherche les primitives de \(\frac{y’}{y}\), qui est de la forme \(\frac{u’}{u}\), et les primitives de \(\frac{u’}{u}\) sont les fonctions \(\ln|u|\).

Exemple

L’équation \( y’=-5y\) admet pour solutions les fonctions: $$y(x)=C\text{e}^{5x},\ C\in\mathbb{R}.$$Il y a donc une infinité de solutions.

Résolution de y‘ + ay = f(x)

Cette équation se résout en deux temps.

• D’abord, on résout l’équation sans second membre y‘ + ay = 0 à l’aide de ce que l’on a dit précédemment; cette équation admet pour solutions les fonctions \(y_0(x)=C\text{e}^{-ax},\ C\in\mathbb{R}\).
• Ensuite on trouve une solution particulière, c’est-à-dire une fonction \(y_p\) telle que \(y_p^\prime(x)+ay_p(x)=f(x)\).
• L’ensemble des solutions de l’équation différentielle sera l’ensemble des fonctions \(y(x)=y_0(x)+y_p(x)\).

Exemple : y‘ – 3y = x²

L’équation homogène associée à cette équation est y‘ – 3y = 0, admettant \(y_0(x)=C\text{e}^{3x}\, C\in\mathbb{R}\) comme solutions.

De plus, le second membre de l’équation différentielle étant un polynôme de degré 2, une solution particulière peut être un polynôme de degré 3 (car une fois dérivé, cela donnera un polynôme de degré 2).

Posons alors \(y_p(x)=ax^3+bx^2+cx+d\); ainsi, \(y_p^\prime(x)=3ax^2+2bx+c\). Donc:$$\begin{align} & y_p^\prime(x)-3y_p(x)=x^2\\\iff& 3ax^2+2bx+c-3(ax^3+bx^2+cx+d)=x^2\\\iff& -3ax^3+(3a-3b)x^2+(2b-3c)x+c-3d=x^2\\\iff&\begin{cases} -3a=0\\3a-3b=1\\ 2b-3c=0\\c-3d=0\end{cases}\\\iff&a=0,\ b=-\frac{1}{3},\ c=-\frac{2}{9},\ d=-\frac{2}{27}.\end{align}$$Donc \(y_p(x)=-\frac{1}{3}x^2-\frac{2}{9}x-\frac{2}{27}\).

Ainsi, les solutions de l’équation différentielle initiale sont:$$y(x)=
-\frac{1}{3}x^2-\frac{2}{9}x-\frac{2}{27} + C\text{e}^{3x}\, C\in\mathbb{R}.$$

Équation de la forme ay » + by + c = 0

Équation caractéristique

Ce genre d’équation différentielle est souvent accompagné de son équation caractéristique. Pour obtenir l’équation caractéristique, on remplace y » par r² et y par r; on obtient alors ar²+br+c=0, équation du second degré bien connue. On arrive alors à démontrer que les solutions de l’équation différentielles sont de la forme \( A\text{e}^{r_1x} +B\text{e}^{r_2x}\), où \(r_1\) et \(r_2\) sont les solutions (réelles ou complexes) de l’équation caractéristique.

On obtient ainsi le théorème suivant.

Solutions

• si \(\Delta=b^2-4ac<0\) alors les solutions sont:$$y(x)=\big[A\cos(\beta x)+B\sin(\beta x)\big]\text{e}^{\alpha x},\ A,B\in\mathbb{R}$$où \(\alpha=-\frac{b}{2a}\) et \(\beta=\frac{\sqrt{|\Delta|}}{2a}\).
• si \(\Delta=0\) alors les solutions sont:$$y(x)=(Ax+B)\text{e}^{rx},\ A,B\in\mathbb{R}$$où \(r=-\frac{b}{2a}\).
• si \(\Delta>0\) alors les solutions sont:$$y(x)=A\text{e}^{r_1x}+B\text{e}^{r_2x},\ A,B\in\mathbb{R}$$où \(r_1\) et \(r_2\) sont les racines du polynôme ax²+bx+c.

Un cas particulier : l’équation \(y »+\omega^2y=0\)

Les solutions sont, d’après le théorème vu précédemment:$$y(x)=A\cos(\omega x)+B\sin(\omega x).$$

Bonus : avec second membre

Si l’équation est de la forme ay » + by + c = f(x) alors pour la résoudre, on fera la même chose que pour les équations du premier ordre : somme des solutions de l’équation homogène associée et d’une solution particulière.

Les applications des équations différentielles

Loi de Malthus

Considérons une culture de bactéries en milieu clos. La loi de Malthus est un modèle d’évolution disant que la vitesse d’accroissement des bactéries est proportionnelle au nombre de bactéries présentes. Ainsi, y‘ = ay, où y(t) représente le nombre de bactéries à l’instant t.

Dans la pratique, ce modèle n’est pas vraisemblable. On lui préférera le modèle de Verhulst:$$y’=ay(M-y)$$mais cette équation n’étant pas linéaire, je n’en parlerai pas ici (peut-être dans un autre article).

Dans un circuit électrique

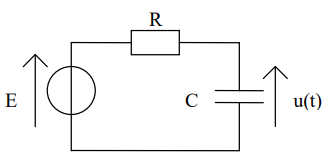
On considère un circuit électrique où u(t) est la tension électrique aux bornes d’un condensateur C alimenté à travers une résistance R sous une tension constante E.

Les lois de l’électricité indiquent que:$$RCu’+u=E.$$Ainsi, pour trouver la tension, on doit résoudre une équation différentielle.

Oscillation mécanique

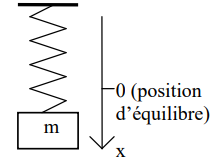
Considérons une masse m suspendue à un ressort de constante de raideur k. x désigne la position de la masse par rapport à sa position d’équilibre. Le frottement est supposé proportionnel à la vitesse v = x’(t). λ est le coefficient de frottement (λ>0).

Les lois de la mécanique du mouvement nous indiquent que:$$m⋅x’’(t) + λ⋅x’(t) + k⋅x(t) = 0.$$Ainsi, pour trouver la position de la masse, il faut résoudre une équation différentielle.