Comment mélanger le calcul littéral, la géométrie (dans un cercle) et mettre le tout dans une démonstration? Oui, je sais que le résultat auquel nous allons aboutir n’est plus au programme du collège, mais cela n’empêche pas de se pencher sur sa démonstration, qui fait intervenir le calcul littéral (qui est encore au programme… profitons-en!).

J’ai un élève en cours particulier qui est en classe de 4ème et il aborde le calcul littéral. Comme il comprend plutôt bien les choses, j’ai décidé de faire avec lui une activité qui lui montre que le calcul littéral peut aussi servir à démontrer des résultats géométriques.

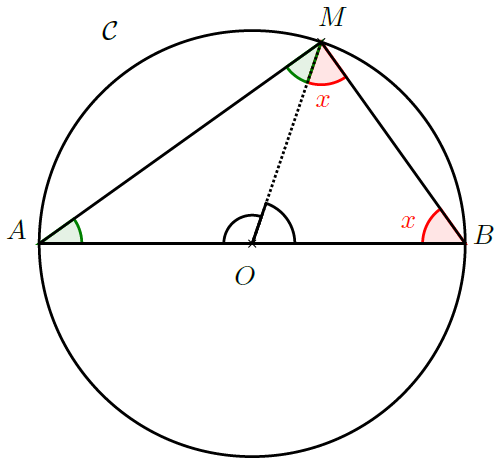
J’ai donc construit cette activité, qui démontre un résultat disparu des programmes. Ce résultat dit que tout triangle inscrit dans un cercle dont un côté coïncide avec un diamètre est rectangle.

Démonstration dans un cercle avec le calcul littéral: l’activité

J’avais envie d’y aller doucement. J’ai donc repris les notions de géométrie qui ont pu être abordées en classes antérieures concernant les triangles et les angles.

C’est la raison pour laquelle l’activité commence par quelques questions succinctes. On y reprend le vocabulaire de base (segment, longueur, angles adjacents, angles supplémentaires, mesure d’un angle, triangle isocèle). J’ai toujours insisté sur la différence qu’il y a entre « angles » et « mesure d’angle ». Un angle est un objet géométrique alors que sa mesure est un objet numérique. Ce dernier peut dont être représenté par une lettre quand on ne la connait pas (calcul littéral).

Pour les abonné·e·s de mathweb.fr, vous trouverez ci-dessous le code source \(\LaTeX\).

Bien entendu, tout commentaire est bon à prendre.