Trinôme du second degré et Python

Nous allons aborder ici la notion de trinôme du second degré en Python sous un angle POO (Programmation Orientée Objet). J’avais en effet envie de construire une classe Python représentant un tel trinôme et pouvant effectuer toutes les opérations classiques du lycée.

Trinôme du second degré et Python: préliminaires mathématiques

Un trinôme du second degré est un polynôme de la forme:$$P(x)=ax^2+bx+c,\quad a\neq0.$$

À ce polynôme, on peut lui attribuer le nombre:$$\Delta=b^2-4ac$$qui est son discriminant.

Si \(\Delta > 0\) alors il existe deux valeurs distinctes \(x_1\) et \(x_2\) de x telles que P(x) = 0: ce sont les racines de P. Dans ce sas, P(x) peut se factoriser sous la forme \( P(x) = a(x-x_1)(x-x_2) \).

Si \(\Delta = 0\) alors il existe une unique valeur (x_0\) pour laquelle \(P(x_0) = 0\): c’est sa racine double. Sans ce cas, \( P(x)=a(x-x_0)^2\).

Si \(\Delta < 0\) alors l’équation P(x) = 0 n’admet aucune racine réelle, et P(x) ne se factorise pas dans l’ensemble des nombres réels.

À l’aide de la forme factorisée de P(x), si elle existe, on peut déduire le signe de P(x).

Je vous invite à regarder la fiche de cours sur le second degré sur cette page.

Trinôme du second degré et Python: préliminaires informatiques

J’avais d’abord publié un article dans lequel j’exposais des méthodes plutôt longues… Et puis, après quelques recherches, j’ai découvert que je pouvais utiliser Xcas avec Python ! Cela tombe bien car cela facilite beaucoup la construction des méthodes.

Python et giac Xcas

En ligne de commande, il faut avant tout installer les modules Python suivants. Sous windows:

python.exe -m pip install wheel
python.exe -m pip install giacpy

Pour les autres plateformes (MacOS et Linux), allez sur la page suivante pour plus d’informations:

https://www-fourier.ujf-grenoble.fr/~parisse/giac_fr.html

Maintenant, on peut importer les fonctions nécessaires du module giacpy:

from giacpy import latex, solve, simplifier, evalf, factoriser

Ce qu’il y a d’intéressant avec ce module, c’est que l’on va pouvoir effectuer des calculs algébriques. Par exemple:

>>> solve('x*x-3*x+2=0')

est une liste contenant toutes les solution de l’équation \(x^2-3x+2=0\).

Trinôme du second degré et Python: la classe

Le constructeur

class Trinome:
    def __init__(self,a,b,c):
        self.a = a
        self.b = b
        self.c = c
        self.delta = self.b**2 - 4*self.a*self.c
        self.giac_equation = '{}*x*x+{}*x+{}=0'.format(a,b,c)
        self.giac_trinome = '{}*x*x+{}*x+{}'.format(a,b,c)

J’ai opté pour définir le discriminant dès le constructeur car il ne m’a pas semblé utile d’écrire une méthode rien que pour cela.

Les variables self.giac_… me serviront pour trouver les racines et la factorisation.

Les méthodes

La plupart des méthodes comporte un argument booléen optionnel tex qui permet un retour au format \(\LaTeX\).

• __str__ : pour afficher le polynôme
• racines(tex,approx) : pour calculer les racines (en valeur exacte ou approchée)
• factorise(tex) : pour factoriser le trinôme
• canonique(tex) : pour avoir la forme canonique du trinome
• signe(tex) pour avoir un tableau de signes
• draw(tex,e,namepic) pour dessiner la parabole sur l’intervalle \(\left[-\frac{b}{2a}-e~;~-\frac{b}{2a}+e\right]\) (si tex=True, cela enregistre l’image avec le nom namepic qui, par défaut, est “parabole.png”)
• export_latex(filename) : pour créer un fichier \(\LaTeX\) avec toutes les informations, et qui sera compilé via pdflatex.

Exemples

>>> P = Trinome(-2,3,4)
>>> P.racines()
('(-sqrt(41)+3)/4', '(sqrt(41)+3)/4')
>>> print(P)
-2x²+3x+4
>>> P.canonique()
'-2(x-3/4)² + 41/8'
>>> print(P.signe())
--------------------------------
|  x   |-∞     x₁     x₂     +∞|
--------------------------------
| P(x) |    -   0  +   0  -    |
--------------------------------
>>> P.draw()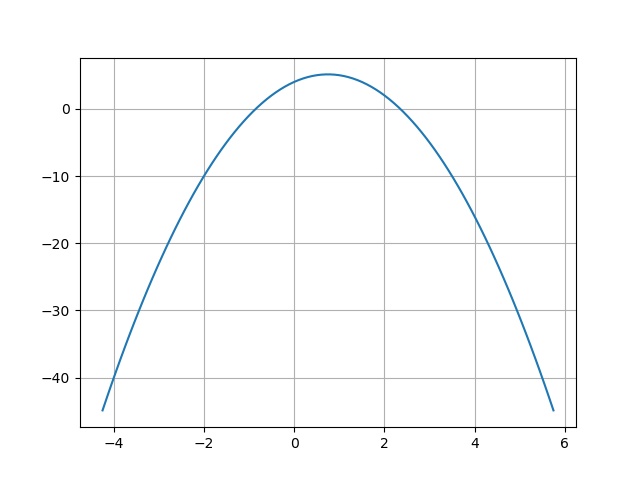

>>> P.export_latex()

qui crée un document .tex et qui génère le PDF suivant:

Téléchargement de la classe