Les carrés de Dirichlet constituent une famille de carrés mathématiquement intéressants.
Nulle question ici de géométrie, mais plutôt d’arithmétique…
Carrés de Dirichlet: définition
En une phrase, on pourrait définir un carré de Dirichlet comme une grille (carrée) de nombres où chacun des nombres est la moyenne des nombres se trouvant au-dessus, en dessous, à droite et à gauche. Par exemple:
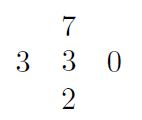
Le nombre « 4 » est la moyenne arithmétique des quatre nombres 7, 3, 0 et 2:$$3 = \frac{7+3+0+2}{4}.$$
Bien entendu, vous vous en doutez, il y aura un léger soucis aux bords de la grille; c’est la raison pour laquelle figurent des nombres à l’extérieur du carré.
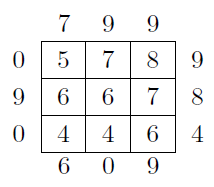
Voici un exemple complet:
\documentclass{article}
\usepackage{array,cellspace}
\setlength{\cellspacetoplimit}{4pt}
\setlength{\cellspacebottomlimit}{4pt}
\begin{document}
\begin{tabular}{c|Sc|Sc|Sc|c}
\multicolumn{1}{c}{} & \multicolumn{1}{c}{7} & \multicolumn{1}{c}{9} & \multicolumn{1}{c}{9} & \\\cline{2-4}
0 & 5 & 7 & 8 & 9 \\\cline{2-4}
9& 6 & 6 & 7 & 8 \\\cline{2-4}
0 & 4 & 4 & 6 & 4 \\\cline{2-4}
\multicolumn{1}{c}{} & \multicolumn{1}{c}{6} & \multicolumn{1}{c}{0} & \multicolumn{1}{c}{9} & \\
\end{tabular}
\end{document}
Un premier résultat sur les carrés de Dirichlet
Tous les nombres à l’intérieur du carré de Dirichlet sont inférieurs ou égaux au maximum de ceux qui se trouvent à l’extérieur.
Si l’on regarde l’exemple précédent, le maximum des nombres se trouvant à l’extérieur est égal à 9. On constate bien que tous les nombre à l’intérieur du carré sont inférieurs ou égaux à 9.
Pourquoi est-ce vrai ? On peut raisonner par l’absurde. Supposons que le maximum soit à l’intérieur, et notons-le « M ». Pour plus de facilité dans les explications, je vais désigner par « les nombres autour » ceux qui se trouvent au-dessus, en dessous, à droite et à gauche.
Alors, comme moyenne de quatre nombres, M est inférieur ou égal aux nombres qui l’entourent. Mais comme il est le maximum de la grille, il est nécessairement égal à tous les nombres qui l’entourent. On se retrouve donc localement avec un schéma comme celui-ci:
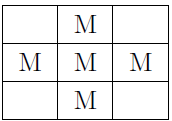
Par un raisonnement analogue sur les autres cases (qui contiennent M), on arrive à voir que nécessairement, le carré de Dirichlet ne comporterait que des M.
Unicité du carré de Dirichlet
Étant donnés des nombres à l’extérieur du carré de Dirichlet, il n’existe qu’une seule façon de le compléter.
Pour s’en convaincre, on va considérer deux carrés de Dirichlet d’ordre 2 ayant les mêmes nombres extérieurs, mais pas nécessairement les mêmes nombres intérieurs:
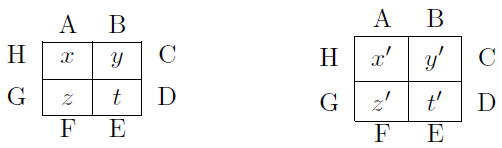
Considérons maintenant un autre carré de mêmes dimensions où tous les nombres sont les différences de ceux du deuxième et ceux du premier :
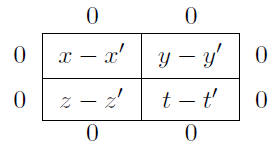
Souvenons-nous maintenant que nous avions les égalités suivantes:$$\begin{cases}x = \frac{A+B+y+z}{4}\\x’=\frac{A+H+y’+z’}{4}\end{cases}$$Donc:$$x-x’=\frac{0 + 0 + (y-y’) + (z-z’)}{4}.$$
Donc \(x-x’\) est la moyenne des quatre nombres qui l’entourent dans le dernier carré.
Il en est de même pour les trois autres nombres intérieurs de ce dernier carré. Donc c’est un carré de Dirichlet.
D’après le « principe du maximum » vu dans la section précédente, cela signifie que « 0 » est le maximum de tous les nombres de ce carré, et donc que \(x=x’\), \(y=y’\), \(z=z’\) et \(t=t’\).
Cela montre donc que la solution d’un carré de Dirichlet est unique.
Une méthode pour compléter un carré de Dirichlet
Étape initiale pour la résolution des carrés de Dirichlet
Nous allons chercher à compléter le carré de Dirichlet suivant :
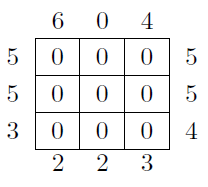
J’ai inséré des « 0 » à l’intérieur par défaut, mais ils vont très vite disparaître.
L’idée est de se dire que ceci n’est que l’étape initiale d’un (long) processus. Appelons-la l’étape 0.
Étape 1
L’étape suivante consiste à transformer le premier « 0 » (en haut à gauche) en la moyenne des nombres qui l’entourent.
Il devient alors (6 + 5 + 0 + 0)/4 = 2,75.
On passe alors au « 0 » qui se trouve à sa droite, qui se transforme en (0 + 2,75 + 0 + 0)/4 = 0,5375.
Ensuite, on passe au « 0 » à sa droite, qui devient : (4 + 0,5375 + 0 + 5)/4.
On parcourt ainsi toute la grille de haut en bas, de gauche à droite.
Étape 2
Si les nombres intérieurs obtenus à l’étape précédente ne sont pas tous égaux à la moyenne des nombres qui les entourent, on recommence… jusqu’à obtenir ce que l’on veut.
Implémentation en Python
square = [[0, 6, 0, 4, 0],
[5, 0, 0, 0, 5],
[5, 0, 0, 0, 5],
[3, 0, 0, 0, 4],
[0, 2, 2, 3, 0]]
def dirichlet_square_solver():
end = True
for line in range(1,len(square)-1):
for col in range(1,len(square)-1):
temp = square[line][col]
square[line][col] = ( square[line-1][col] + square[line][col-1] + square[line][col+1] + square[line+1][col] ) / 4
if square[line][col] != temp:
end = False
if not end:
dirichlet_square_solver()
else:
c = ''
for line in range(len(square)):
for col in range(len(square)):
c += '{:^5}'.format(square[line][col])
c += '\n'
print(c)
dirichlet_square_solver()
0 6 0 4 0
5 4.5 3.0 4.0 5
5 4.0 3.5 4.0 5
3 3.0 3.0 3.5 4
0 2 2 3 0 Pourquoi cette méthode fonctionne ?
Notons \(x^{(k)}_n\) les suites de nombres définies ainsi:

\(x^{(k)}_1\) est la moyenne des nombres qui l’entourent, donc sa valeur sera nécessairement plus grande que 0. Donc à la fin de l’étape 1, toutes les valeurs intérieures seront plus grandes que les valeurs initiales.
On comprend alors qu’à la fin de l’étape n, toutes les valeurs de \(x^{(k)}_n\) seront supérieures à celles de l’étape précédente et ainsi de suite (un raisonnement par récurrence peut nous en convaincre).
Les suites \( (x^{(k)}_n) \) sont donc croissantes. De plus, elles sont toutes majorées (par le maximum, qui est à l’extérieur du carré). Donc, elles convergent vers des limites finies, nécessairement la moyenne des nombres qui les entourent. Ainsi, le carré des valeurs limites est bien un carré de Dirichlet.
Épilogue
Je me suis fortement inspiré de la vidéo d’Olivier Druet, directeur de recherches au CNRS (Institut Camille Jordan, Université Lyon 1).
Vous comprendrez, à travers l’introduction cette vidéo, l’histoire de ce problème, qui n’est autre qu’une histoire de températures.
En effet, supposons que la grille initiale (où l’on ne connaît que les nombres extérieurs) représente un groupe de pièces et que les nombres extérieurs représentent la température dans chacune des pièces « extérieures ». Alors, le carré de Dirichlet représente les températures de chacune des pièces une fois que toutes les pièces aient une température constante, moyenne des températures des pièces qui l’entourent avec lesquelles elle a un mur en commun… Ouais, je sais, je n’explique pas super bien… les transferts thermiques ne sont clairement pas ma spécialité !…



c’est un peu fastidieux comme méthode. il n’y a pas plus simple?
remarque : il y a des erreurs de calculs, notamment (7+3+0+2)/4 c’est 3 et pas 4.
Merci pour le signalement de l’erreur de calcul. Cela dit, mettre « erreurs » (au pluriel) me rend perplexe car je n’ai vu que cette erreur 🙂
Quant à la fastidiosité, c’est selon l’appréciation de tout un chacun.C’est une méthode algorithmique où il faut seulement faire la moyenne de quatre nombres. On a vu pire je crois 🙂
Maintenant, si vous parlez du programme (et non de la méthode), on peut toujours imaginer autre chose. Chaque programme ressemble à la personne qui l’écrit.
Petite rectification (sans trop d’importance):
M n’est pas « inférieur ou égal aux nombres qui l’entourent ». Disons que, soit ils lui sont tous égaux, soit il en existe au moins un qui lui soit strictement supérieur ce qui contredirait l’hypothèse de sa maximalité. Donc ils lui sont tous égaux. (Et de proche en proche, on montre qu’alors tous les coefficients intérieurs ou extérieurs sont égaux à M.)