Je vais ici vous proposer un exercice où il est question de tangentes à un cercle et de droites concourantes dont la solution fait appel à un résultats mathématique peu connu: le théorème de Ceva.
Tangentes à un cercle et droites concourantes: l’énoncé
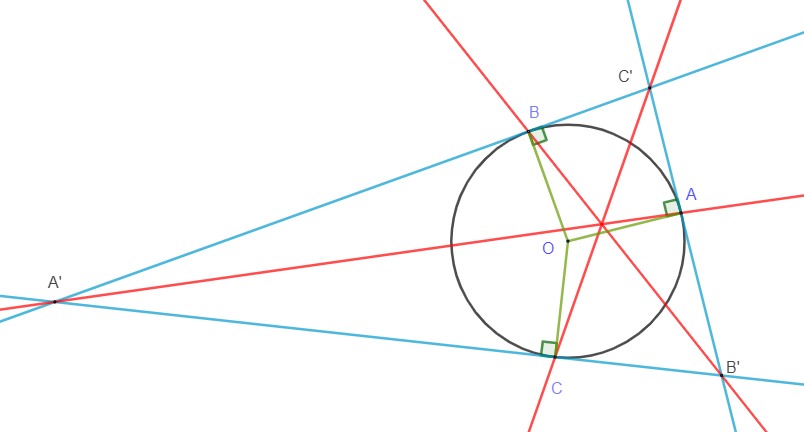
On considère un cercle \(\mathcal{C}\) de centre O, et trois points A, B, C sur ce cercle, non diamétralement opposés deux à deux. Autrement dit, [AB], [AC] et [BC] ne sont pas des diamètres de \(\mathcal{C}\).
On trace alors les tangentes \(T_A\), \(T_B\) et \(T_C\) à \(\mathcal{C}\) respectivement en A, B et C.
\(T_A\) et \(T_B\) se coupent en C’,
\(T_A\) et \(T_C\) se coupent en B’,
\(T_B\) et \(T_C\) se coupent en A’.
Montrer que (AA’), (BB’) et (CC’) sont concourantes, c’est-à-dire qu’elles se coupent en un unique point.
Tous les niveaux de résolution sont acceptés.
Vous pourrez proposer votre solution en commentaire. Celui-ci ne sera pas publié s’il comporte des erreurs mathématiques. En revanche, s’il est correct, il apparaitra dans la section suivante de façon anonyme si vous le souhaitez (dans ce cas, merci de le préciser dans votre commentaire).
Tangentes à un cercle et droites concourantes: une figure
Tangentes à un cercle et droites concourantes: le fichier geogebra
Tangentes à un cercle et droites concourantes: une solution
Préliminaires
Par construction, les triangles OAC’ et OBC’ sont rectangles respectivement en A et B, ont un côté en commun, le segment [OC’], et deux côtés de même mesure, à savoir OA = OB. Ainsi, ils sont semblables et on peut alors conclure que AC’ = BC’.
Par un raisonnement analogue, on peut démontrer que CA’ = BA’ et CB’ = AB’.
Notion de barycentres
Notons:$$\alpha=AC’=BC’\quad,\quad \beta=BA’=CA’\quad,\quad\gamma=CB’=AB’.$$
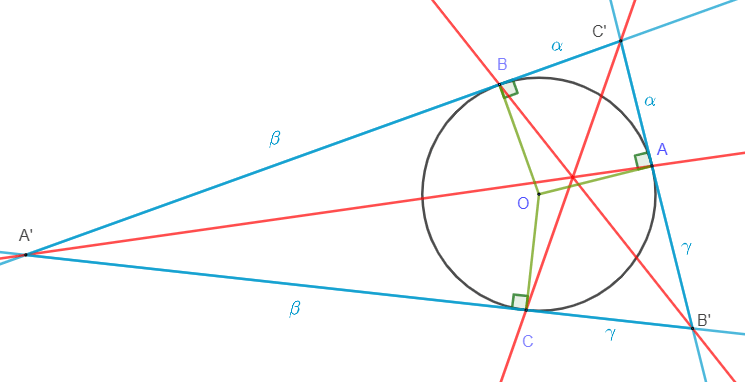
On peut écrire:$$\gamma \vec{AC’} + \alpha\vec{AB’}=\vec{0}.$$On dit alors que A est le barycentre du système pondéré \( \{(B’;\alpha),(C’;\gamma)\}\), et on peut noter:$$A=\text{bar}\{ (B’;\alpha),(C’;\gamma) \}.$$
En multipliant l’égalité vectorielle par \(\beta\), on a:$$\beta\gamma \vec{AC’} + \alpha\beta\vec{AB’}=\vec{0}.$$Autrement dit:$$A=\text{bar}\{ (B’;\alpha\beta),(C’;\beta\gamma) \}.\quad\quad(1)$$
On peut alors démontrer de même que:$$B=\text{bar}\{ (A’;\alpha\gamma),(C’;\beta\gamma) \}\quad\quad(2)$$et$$C=\text{bar}\{ (A’;\alpha\gamma),(B’;\alpha\beta) \}.\quad\quad(3)$$
Considérons maintenant le point I définit ainsi:$$I=\text{bar}\{ (A’;\alpha\gamma), (B’;\alpha\beta),(C’;\beta\gamma) \}.$$
Associativité du barycentre
Posons:$$N=\text{bar}\{ (P;a),(Q;b) \}$$avec\(a+b\neq0\). Alors,$$a\vec{NP}+b\vec{NQ}=\vec{0}.$$
Posons maintenant $$M=\text{bar}\{ (P;a),(Q;b),(R,c) \}$$Alors:$$\begin{array}{ll} & a\vec{MP}+b\vec{MQ}+c\vec{MR}=\vec{0}\\\iff & a\big(\vec{MN}+\vec{NP}\big)+b\big(\vec{MN}+\vec{NQ}\big)+c\vec{MR}=\vec{0}\\\iff & (a+b)\vec{MN}+\underbrace{a\vec{NP}+b\vec{NQ}}_{=\vec{0}}+c\vec{MR}=\vec{0}\\\iff & (a+b)\vec{MN}+c\vec{MR}=\vec{0}\\\iff & M=\text{bar}\{ (N;a+b),(R;c) \} \end{array} $$
Ce dernier résultat est appelé l’associativité du barycentre.
Retour au problème
On a:$$\left.\begin{array}{l}I=\text{bar}\{ (A’;\alpha\gamma), (B’;\alpha\beta),(C’;\beta\gamma) \}\\A=\text{bar}\{ (B’;\alpha\beta),(C’;\beta\gamma) \} \end{array}\right\}\Rightarrow I=\text{bar}\{ (A’;\alpha\gamma),(A;\alpha\beta+\beta\gamma) \}$$
On peut alors dire que:$$I\in(AA’).$$
De même,$$\left.\begin{array}{l}I=\text{bar}\{ (A’;\alpha\gamma), (B’;\alpha\beta),(C’;\beta\gamma) \}\\B=\text{bar}\{ (A’;\alpha\gamma),(C’;\beta\gamma) \} \end{array}\right\}\Rightarrow I=\text{bar}\{ (B’;\alpha\beta),(B;\alpha\gamma+\beta\gamma) \}$$ et $$\left.\begin{array}{l}I=\text{bar}\{ (A’;\alpha\gamma), (B’;\alpha\beta),(C’;\beta\gamma) \}\\C=\text{bar}\{ (A’;\alpha\gamma),(B’;\alpha\beta) \}\end{array}\right\}\Rightarrow I=\text{bar}\{ (C’;\beta\gamma),(C;\alpha\beta+\alpha\gamma) \}$$
On en conclut alors que \( I\in(BB’)\) et \(I\in(CC’)\).
Par conséquent, I est le point d’intersection des droites (AA’), (BB’) et (CC’).
Théorème de Ceva
Ce que nous venons de démontrer est un cas particulier du théorème de Ceva.
Vous en saurez plus sur ce théorème en regardant la page wikipedia.


