Calculer le volume d’un tronc de cylindre couché est l’un des objectifs principaux de l’exercice que nous allons voir dans cet article.
Calculer le volume d’un tronc de cylindre couché: l’énoncé
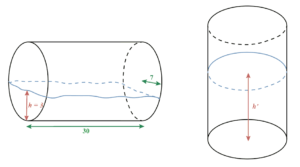
Nous disposons d’une citerne cylindrique couchée dans laquelle est mis un certain volume d’eau.
Ce que nous savons:
- le rayon de la base de la citerne est égal à 7 unités;
- sa hauteur est égale à 30 unités;
- la hauteur de l’eau s’élève à h = 3 unités.
On relève la citerne de 90°.
Question: quelle est la hauteur h’ de l’eau dans la citerne une fois relevée ?
Calculer le volume d’un tronc de cylindre couché: résolution de l’exercice
Calculer le volume d’un tronc de cylindre couché: volume d’eau
Pour pouvoir répondre à cette question, il nous faut calculer le volume d’eau, et donc le volume d’un tronc de cylindre couché.
Si on regarde la citerne couchée, la vue de face donne ceci:
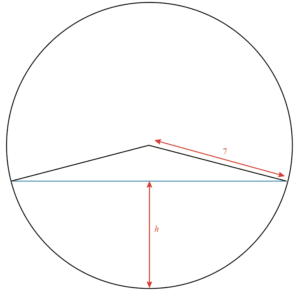
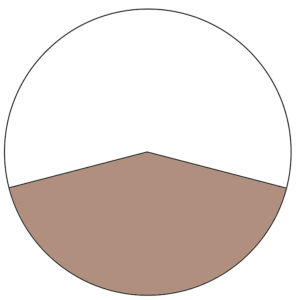
Cette question revient donc à trouver avant tout l’aire de la surface « coincée » entre le cercle et le segment (représentant la surface de l’eau). Pour se faire, considérons le secteur angulaire:
Aire du secteur angulaire
Il nous faut avant tout trouver son aire. Pour cela, il nous faut son angle au centre.
Pour obtenir cet angle, rien de tel qu’un peu de trigonométrie niveau collège:
$$\cos\alpha = \frac{4}{7} \Rightarrow \alpha \approx 55^\circ. $$
Ainsi, l’angle au centre que nous cherchions mesure approximativement 110°. Voilà une bonne chose de faite!
Maintenant, on applique la proportionnalité pour déterminer l’aire du secteur angulaire d’angle au centre 110°:
| Aire du secteur angulaire | Angle du secteur angulaire |
|---|---|
| \( \pi\times7^2 \) | 360° |
| \( x \) | 110° |
Bim, bam, boum, un coup de quatrième proportionnelle (toujours niveau collège) et on trouve: $$x=\frac{110\times49\pi}{360}\approx 47.$$
Aire du triangle isocèle
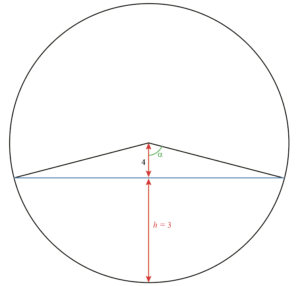
À cette aire, il nous faut enlever l’aire du triangle isocèle de hauteur 4, celui « au-dessus » de l’eau.
À l’aide du théorème de Pythagore, on peut dire que le segment bleu mesure \(2\times\sqrt{7^2-4^2}=2\sqrt{33}.\)
Donc l’aire du triangle isocèle est: \( \frac{2\sqrt{33} \times 4}{2} = 4\sqrt{33} \approx 23. \)
Aire de la section d’eau
L’aire du secteur coincé entre le segment bleu et le cercle est donc environ \(47-23=24\).
Volume d’eau
Maintenant, nous pouvons calculer le volume d’eau en multipliant cette aire par la hauteur du cylindre:$$\mathcal{V}_{\text{eau}}\approx24\times30\approx 720.$$
Calculer le volume d’un tronc de cylindre couché: déterminer la hauteur de l’eau dans la citerne relevée
Une fois que la citerne est relevée, l’eau épouse la citerne (Mazal Tov!) si bien qu’elle a désormais la forme d’un cylindre.
Or, le volume d’un cylindre est: $$\mathcal{V}_{\text{cylindre}}=\pi \times r^2 \times h’.$$Ainsi,$$720 = 49\pi \times h’$$d’où:$$h’=\frac{720}{49\pi}\approx 46,2.$$



Eh bien, j’ai l’impression qu’un détail a été occulté. A mon avis, après avoir calculé l’air du secteur angle d’angle au centre 110°, on devrait y retrancher l’air du triangle délimiter par la ligne bleue et de hauteur 4.
Ensuite seulement on multiplie ce qui reste par la longueur du cylindre pour trouver le volume d’eau. Ensuite on pourra calculer sa hauteur dans le cylindre relevé.
Tout à fait! Le nez collé à l’écran ne me réussit pas… Je viens de rectifier mais n’ayant que très peu de temps, j’ai peut-être fait une erreur de calcul. Il ne faudra pas hésiter à me le dire dans ce cas. Merci pour votre vigilance!
Le calcul est faux car dans l’énoncé il est indiqué « le diamètre de la base est égal à 7 unités » et non « le rayon de la base est égal à 7 unités »
C’était juste une erreur de transcription. Le dessin ne laissait pas de doute. Mais peu importe, ce qui compte, en math, c’est le raisonnement. Mais quand on n’est pas concentré, on peut commettre des erreurs. J’ai rectifié tout de même l’énoncé car il est vrai que c’est mieux sans erreur, quelle qu’elle soit.