Un diagramme de Voronoï (mathématiques et Python), est une représentation graphique. Nous allons voir en quoi elle consiste.

Pour celles et ceux qui désirent en savoir plus, vous pouvez consulter la page wikipedia.

Diagramme de Voronoï: point de vue mathématiques (on verra ensuite pour Python)

Considérons dans un repère orthonormé un système S de points \(A_k(x_k;y_k)\). Le diagramme de Voronoï associé à ce système S permet de voir quels sont les points du plan les plus proches d’un des points de S.

Définitions

L’ensemble:$$\text{Vor}_S(A_k) = \{ M(x;y)\in\mathbb{R}^2,\ MA_k \leqslant MA_i,\ \forall i \neq k\}$$ est l’ensemble des points du plan qui sont plus proches de \(A_k\) que des autres points de S.

Cet ensemble est appelé polygone de Voronoï, ou polygone de Thiessen, du point \(A_k\). On peut aussi l’appeler une cellule.

Le point \(A_k\), quant à lui, est appelé germe (ou centre de la cellule).

Un pavage de Voronoï est l’ensemble des polygones de Voronoï.

En mathématiques

Un pavage de Voronoï avec deux points n’est pas compliqué à trouver. Il s’agit de deux demi-plans délimités par la médiatrice du segment formé par les deux points.

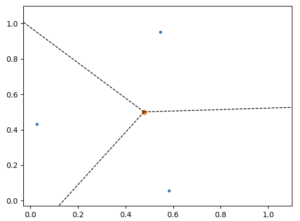
Avec trois points, il suffit de construire les médiatrices des segments formés par ces trois points:

On l’aura compris, il suffit au final de tracer les médiatrices; ce sont elles qui partitionnent le plan pour donner le pavage de Voronoï.

Diagramme de Voronoï: après les mathématiques, une implémentation en Python

Il existe déjà un module qui permet de tracer de tels diagrammes: dans scipy.spatial, il y a une fonction Voronoi.

Premier exemple

import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial import Voronoi, voronoi_plot_2d

points = np.random.rand(10,2) # choisit au hasard 10 points dans le carré unité
vor = Voronoi(points)
fig = voronoi_plot_2d(vor)
plt.show()

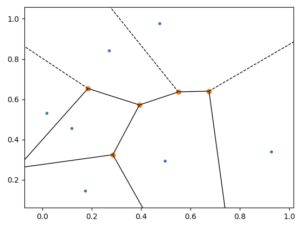
Ce programme choisit 10 points au hasard. Leurs coordonnées sont comprises entre 0 et 1, puis détermine le pavage de Voronoï. On obtient par exemple:

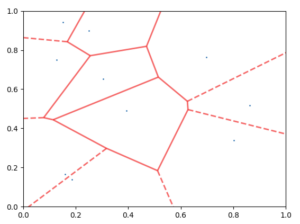
Deuxième exemple

import matplotlib.pyplot as plt
import numpy as np
from scipy.spatial import Voronoi, voronoi_plot_2d

points = np.random.rand(10,2)
vor = Voronoi(points)
fig = voronoi_plot_2d(vor, show_vertices=False, line_colors='red',line_width=2, line_alpha=0.6, point_size=2)
plt.show()

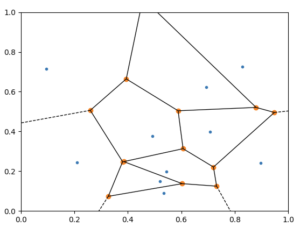
Note : j’ai oublié de mettre à l’échelle les graphiques précédents, donc il est normal que les bords des polygones ne semblent pas perpendiculaires aux segments joignant deux points du système. L’orthogonalité se verra mieux sur les graphiques suivants.

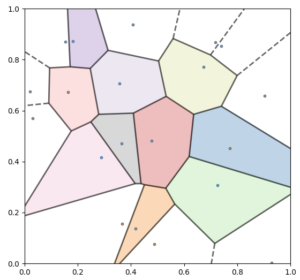
Troisième exemple: avec de la couleur (c’est plus fun!)

import numpy as np
from scipy.spatial import Voronoi, voronoi_plot_2d
import matplotlib.pyplot as plt

points = np.random.rand(20, 2)
vor = Voronoi(points)
colors = plt.cm.tab20(np.arange(len(vor.regions)))

fig, ax = plt.subplots()
voronoi_plot_2d(vor, ax=ax, show_vertices=False, line_colors='k', line_width=2, line_alpha=0.6)


for region_index, region in enumerate(vor.regions):
    if not -1 in region and len(region) > 0:  # Vérifier si la région est finie
        polygon = [vor.vertices[i] for i in region]
        ax.fill(*zip(*polygon), color=colors[region_index], alpha=0.3)

# Ajouter les points d'origine
ax.plot(points[:, 0], points[:, 1], 'o', markersize=1)

# Optionnel : ajuster les limites de la figure pour mieux voir le pavage
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)

plt.show()

Applications du diagramme de Voronoï

La polyvalence des diagramme de Voronoï en fait un outil puissant. Dans l’analyse et la modélisation de structures spatiales dans de nombreux domaines scientifiques et appliqués, par exemple:

• Sciences géospatiales : pour diviser une région en zones contiguës en fonction de la proximité des points de données. Cela peut être utile dans la cartographie, la télédétection, la géologie, etc.
• Planification des réseaux : dans les télécommunications, pour planifier l’emplacement des tours de téléphonie mobile. Cela permet de maximiser la couverture du signal et minimiser les chevauchements.
• Modélisation des mouvements de particules : en physique et en biologie, pour modéliser le déplacement des particules. Cela se fait dans un espace en fonction des attracteurs ou des obstacles présents.
• Traitement d’images : pour segmenter les images en régions homogènes en fonction des niveaux de gris ou des couleurs.
• Optimisation : dans des problèmes d’optimisation pour diviser l’espace en régions qui minimisent la distance à un ensemble de points donnés.
• Modélisation des écosystèmes : pour modéliser les territoires de chasse ou de recherche des animaux en fonction de leur emplacement.
• Analyse des données spatiales : analyser la distribution spatiale des données. Cela permet d’identifier les clusters, les zones denses ou les régions isolées.
• Conception architecturale : pour générer des motifs de conception spatiale. Mais aussi pour déterminer la répartition des espaces en fonction des besoins des utilisateurs.