Créer un GIF avec LaTeX, Python et ImageMagick
Créer un GIF avec LaTeX, Python et ImageMagick, comment faire ?
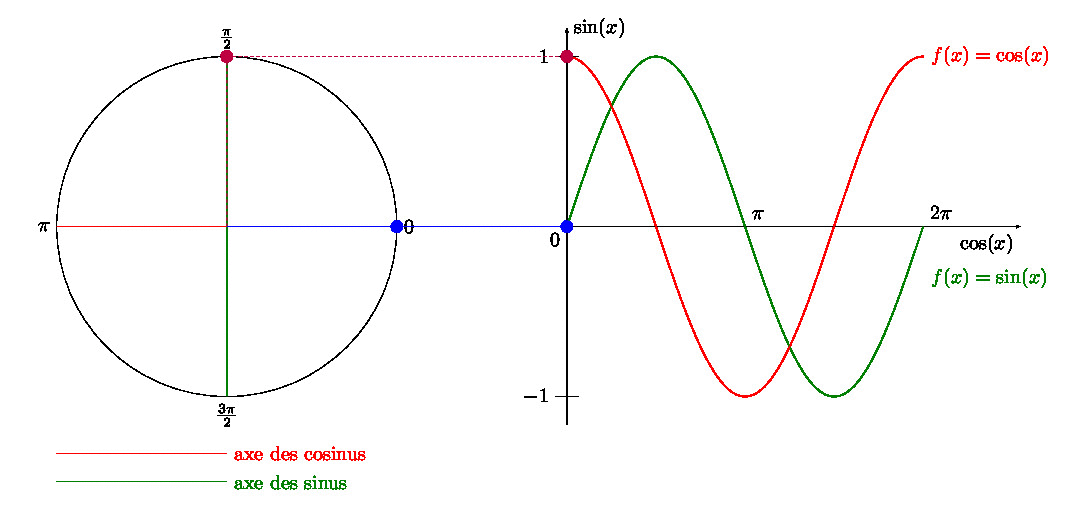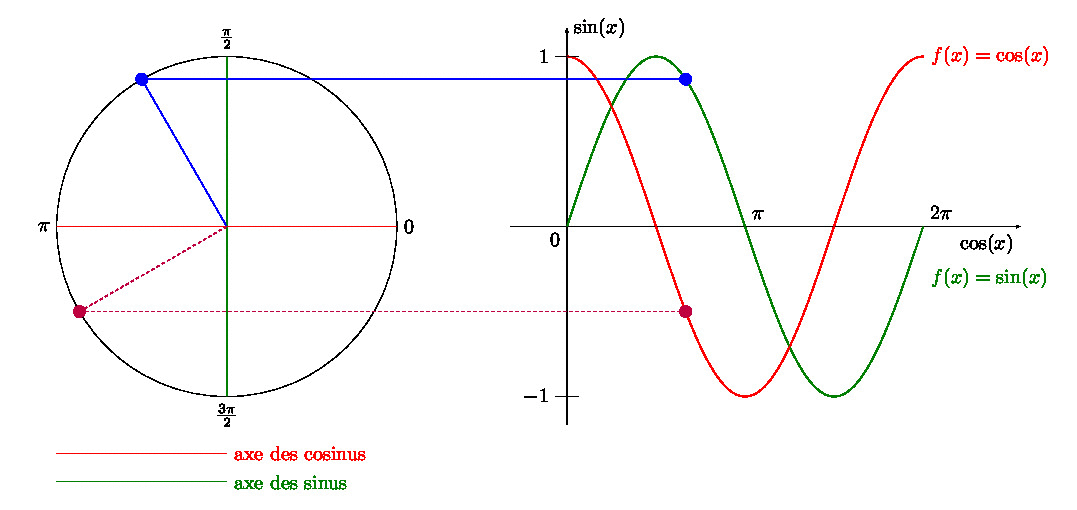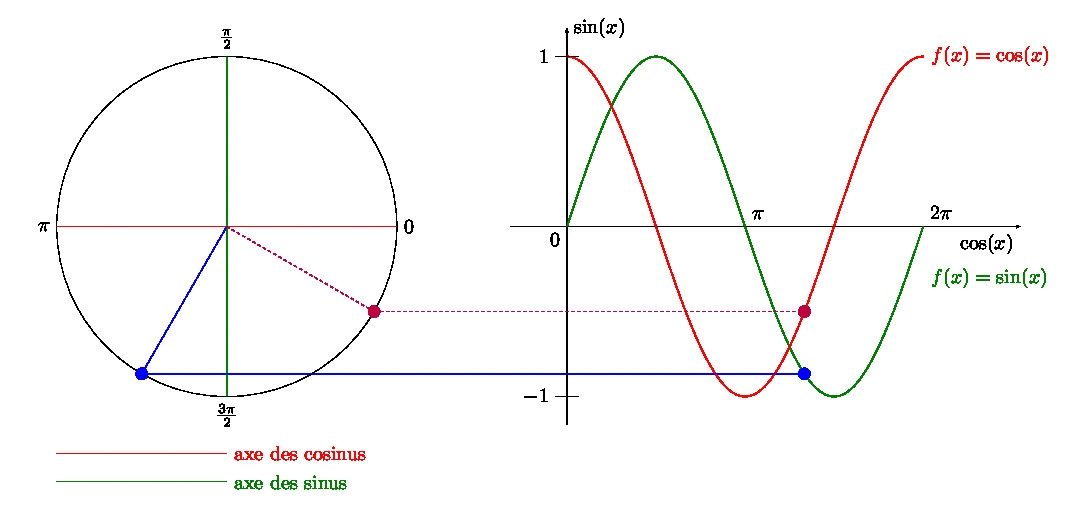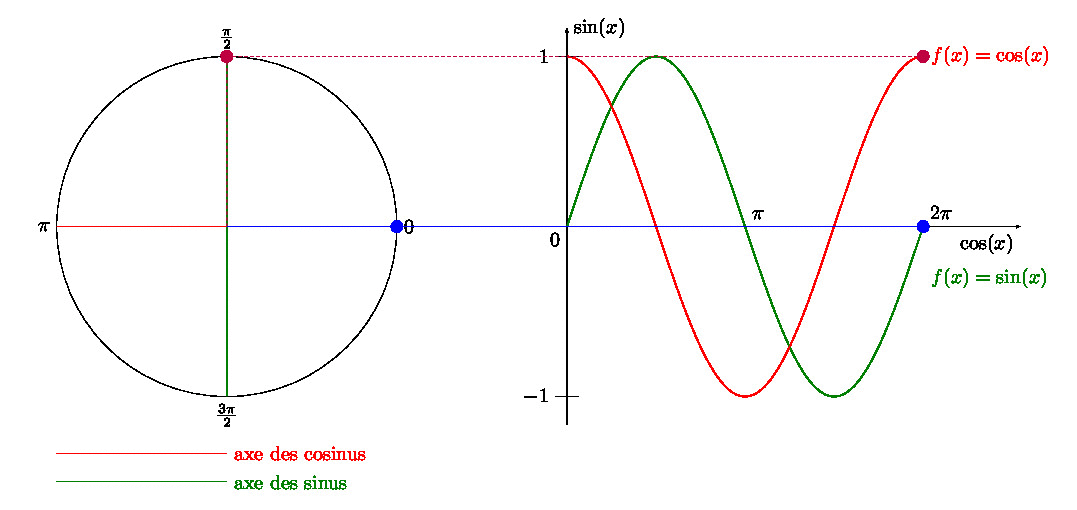
Dans un article précédent, je vous expliquais comment créer un GIF avec \(\LaTeX\), et avec une manipulation Gimp. Trouvant la dernière étape un peu… (comment dire pour rester poli ?) … pénible, je vous propose un combi \(\LaTeX\) + Python + ImageMagick.
(suite…)Créer des animations GIF avec Geogebra : mission impossible ?
Geogebra n’est plus à présenter. Ce logiciel de géométrie (entre autre) permet quelque fois de présenter en cours des choses plutôt sympas.
Dans cet article, je vais prendre pour prétexte une activité que j’avais proposée à mes élèves de 6ème afin de créer une animation et au final, un Gif.
Sources LaTeX des Gifs animés
Convergence de la loi binomiale Téléchargez le fichier source Construire une droite parallèle Téléchargez le fichier source Le flocon de Von Koch Téléchargez le fichier source
Gifs animés
On peut créer des GIFs (animés… oui, c’est un pléonasme) avec beaucoup de logiciels, y compris en ligne. Mais quand on a une idée bien précise de ce que l’on veut faire et qu’on sait créer les dessins avec \(\LaTeX\), il est dommage de se casser la tête pour rien… […]
Epreuve de mathématiques en première
C’est officiel: il y aura une épreuve anticipée de mathématiques en première dès 2026, et cette épreuve comptera pour le bac 2027.
(suite…)Jeux de réflexion faits en Python
J’ai conçu des jeux de réflexion en Python: vous les trouverez ci-dessous. Le Memory’Pix Game Ce jeu permet de tester et de développer sa mémoire à court terme. Sudoku Ce jeu construit une grille de Sudoku et sa solution, et permet une exportation au format image et PDF (via \(\LaTeX\)). Les […]
Un chiffrement d’images avec python
Je vous présente ici une méthode de chiffrement personnel d’images avec Python. Pour se faire, nous allons prendre une image quelconque, par exemple celle-ci:
(suite…)Un jeu de mémoire en Python
J’ai créé en Python un jeu de mémoire. Comme je m’ennuie en ce moment, je comble mon temps en écrivant des programmes.
Pour cela, j’ai voulu m’aider de ChatGPT nouvelle version… J’aurais mieux fait de me casser une jambe, mais bon! Ce qui est fait est fait…
(suite…)Trouver le point du cercle pour lequel la distance totale est minimale
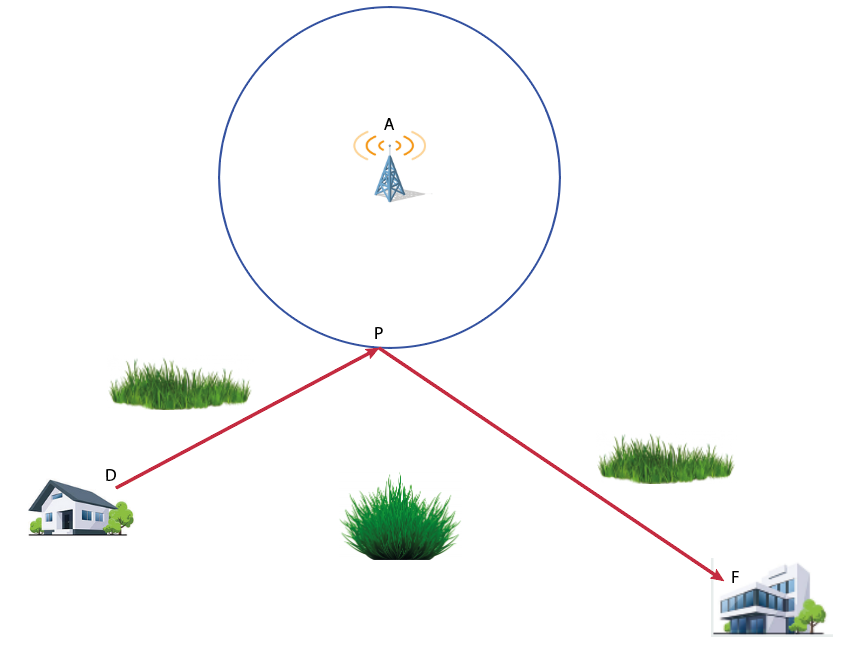
Je me trouve à mon domicile (D), en pleine campagne où il n’y a pas de réseau téléphonique.
Je dois me rendre chez mon ami Fabien (F), isolé lui aussi. Mais comme je suis une personne polie, je souhaite appeler Fabien afin de le prévenir de ma venue. Je dois donc me rendre au point (P) le plus proche possible de chez moi où il y a du réseau (donc sur le cercle de centre A, où A est l’antenne réseau) de sorte à minimiser la distance totale que je devrai parcourir (donc minimiser DP + PF).
La question est la suivante: où doit se trouver le point P ?
(suite…)



