Dans les années 1940, les mathématiciens Edward Kasner et James Roy Newman découvrirent une constante :
\[ R=\frac{1}{\cos\left(\frac{\pi}{3}\right)\times\cos\left(\frac{\pi}{4}\right)\times\cos\left(\frac{\pi}{5}\right)\times\cdots} \]
que l’on peut aussi écrire : \[ R=\prod_{n\geq3}\frac{1}{\cos\left(\frac{\pi}{n}\right)}.\]

Ils découvrirent cette constante de la manière suivante : on construit successivement :

1. un cercle de rayon r;
2. le triangle équilatéral circonscrit à ce cercle;
3. le cercle circonscrit au triangle équilatéral;
4. le carré circonscrit au dernier cercle;
5. le cercle circonscrit au carré;
6. le pentagone régulier circonscrit au dernier cercle;
7. le cercle circonscrit au pentagone;
8. l’hexagone circonscrit au dernier cercle;
9. etc.

En observant le rayon des cercles, on s’aperçoit que l’on se rapproche de plus en plus d’une valeur proportionnelle à R (définie précédemment).

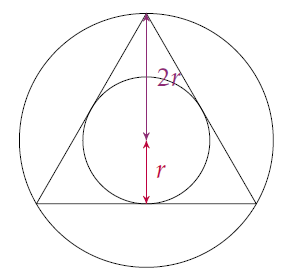
Étape 1

Appelons \(r_0=r\) le rayon du premier cercle et \(r_1\) celui du cercle circonscrit au triangle équilatéral.

Alors, \[r_1= 2r.\]

En effet, le centre d’un cercle inscrit dans un triangle équilatéral est le centre de gravité, qui se trouve aux deux tiers de la médiane en partant du sommet, et ce centre est confondu avec le centre du cercle circonscrit au triangle équilatéral.

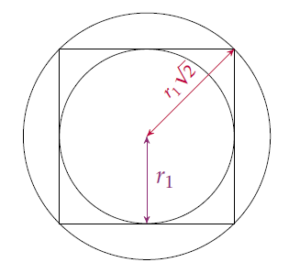
Étape 2

Appelons \(r_2\) le rayon du 3ème cercle.

On a alors : \[r_2=r_1\sqrt{2}\;,\]

c’est-à-dire : \[r_2=2\sqrt{2}r.\]

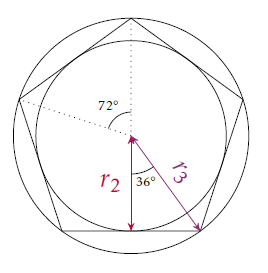
Étape 3

Le pentagone régulier est formé de 5 triangles isocèles de sommets principaux le centre du cercle initial. Donc l’angle au sommet principal dans un de ces triangles isocèles est égal à : \[\frac{360}{5}=72^\circ.\]

Dans un de ces triangles isocèles, la hauteur issue du sommet principal forme deux triangles rectangles identiques dont deux côtés mesurent \(r_2\) (un des côté de l’angle droit), \(r_3\) (l’hypoténuse), et avec un angle de \(\displaystyle\frac{72^\circ}{2}=36^\circ\).

Dans ce triangle rectangle, on a : \[\cos\left(36^\circ\right)=\frac{r_2}{r_3}\]

d’où, en transformant \(36^\circ\) en radians : \[\cos\left(\frac{\pi}{5}\right)=\frac{r_2}{r_3}\]

soit : \[ r_3=\frac{r_2}{\cos\left(\frac{\pi}{5}\right)}=\frac{2\sqrt{2}r}{\cos\left(\frac{\pi}{5}\right)}. \]

Or, \[ \cos\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}=\frac{1}{\sqrt{2}}\qquad\text{et}\qquad\cos\left(\frac{\pi}{3}\right)=\frac{1}{2}\;, \]

d’où : \[ r_3=\frac{r}{\cos\left(\frac{\pi}{3}\right)\cos\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{5}\right)}. \]

Relation de récurrence

Nous le voyons aux étapes précédentes, il s’agit, connaissant \(r_n\), de déterminer \(r_{n+1}\), la distance du centre du polygone régulier à n+3 côtés à l’un de ses sommets. On utilise la même technique qu’à l’étape 3.

L’angle au centre mesure \(\displaystyle\frac{2\pi}{n+3}\) donc, en traçant la hauteur issue du sommet principal du triangle isocèle, on forme un triangle rectangle d’hypoténuse \(r_{n+1}\) et de côté \(r_n\).

On a alors : \[ \cos\frac{\pi}{n+3}=\frac{r_n}{r_{n+1}}\;, \]

soit : \[ r_{n+1}=\frac{r_n}{\cos\frac{\pi}{n+3}}. \]

On déduit de cette relation de récurrence l’égalité : \[ r_n=r\prod_{k=3}^{n+2}\frac{1}{\cos\frac{\pi}{k}}. \]

Convergence

Étudions : \[ \lim\limits_{n\to+\infty}\prod_{k=3}^{n+2}\frac{1}{\cos\frac{\pi}{k}}. \]

Posons \(g(x)=\cos(x) -\left(1 – \frac{x^2}{2}\right)\). Alors, sa dérivée vaut: $$g'(x) = – \sin(x) + x > 0 \quad \forall x > 0.$$ Ainsi, g est croissante. De plus, g(0)=0 donc \(g(x)\geq0\) pour tout réel x strictement positif. D’où, pour tout réel x strictement positif:\[\cos(x)\geq1-\frac{x^2}{2}.\]Ainsi :
$$ \cos(x_1) \cos(x_2) > \left(1 – \frac{x_1^2}{2}\right)\left (1 – \frac{x_2^2}{2}\right)$$ soit: $$ \forall (x_1;x_2)\in(\mathbb{R}_+)^2,\quad \cos(x_1) \cos(x_2) > 1 – \frac{x_1^2}{2} – \frac{x_2^2}{2}.$$ Par récurrence, on en déduit alors que: $$ \cos(x_1) \cos(x_2)\cos(x_3)\ldots > 1 – \frac{x_1^2}{2} – \frac{x_2^2}{2}-\frac{x_3^2}{2} – \cdots $$On en déduit alors: $$\prod_{n \geq 6}{\cos({\pi \over n})} > 1 – {\pi^2 \over 2} \sum_{n \geq 6} {1 \over n^2} = 1 – {\pi^2 \over 2}\left ({\pi^2 \over 6} – \sum_{n \leq 5} {1 \over n^2}\right) \approx 0.105… > 0. $$ Or, $$ \frac{1}{R} = \prod_{n=3}^5\cos\frac{\pi}{n} \times \prod_{n\geq6}\cos\frac{\pi}{n}.$$ Donc \(R < \infty\) car les deux facteurs sont finis et non nuls.

Remarque : nous avons ici utilisé le fait que: $$\prod_{n\geq1}\frac{1}{n^2}=\frac{\pi^2}{6}.$$

Ainsi, malgré les a priori que l’on pourrait avoir, les cercles ont un rayon-limite.

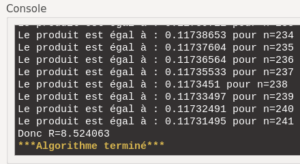
Pour trouver une valeur approchée à \(10^{-4}\) près de ce rayon-limite, en considérant que r = 1 est le rayon du 1er cercle, utilisons Algobox. On arrive alors à une valeur approchée de R définie en introduction.

En Python, cela donne:

from math import pi, cos
p, n, d = 0.5, 3, 10
while (abs(p-d)) > 10**(-5):
    n += 1
    d = p
    p = p * cos(pi/n)
    print("Le produit est égal à {} pour n = {}".format(p,n))
print("Donc R = {}".format(1/p))