Le jeu du 2020
À l’occasion de la nouvelle année qui approche, je vous propose un jeu qui m’a été inspiré directement du nombre 2020…
(suite…)À l’occasion de la nouvelle année qui approche, je vous propose un jeu qui m’a été inspiré directement du nombre 2020…
(suite…)Pour illustrer cette période de Noël, et pour rester tout de même dans la thématique de mon site, rien de tel qu’un code Python pour faire un beau sapin de Noël…
Parce qu’un sapin pourri du genre:
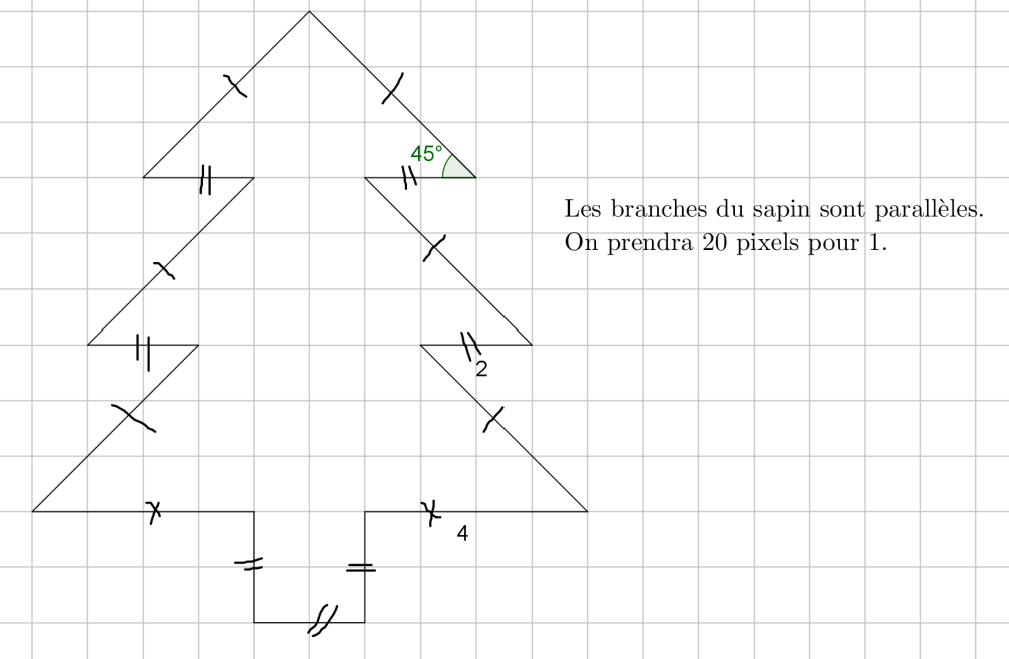
non merci!
(suite…)Créer un GIF avec LaTeX, Python et ImageMagick, comment faire ?
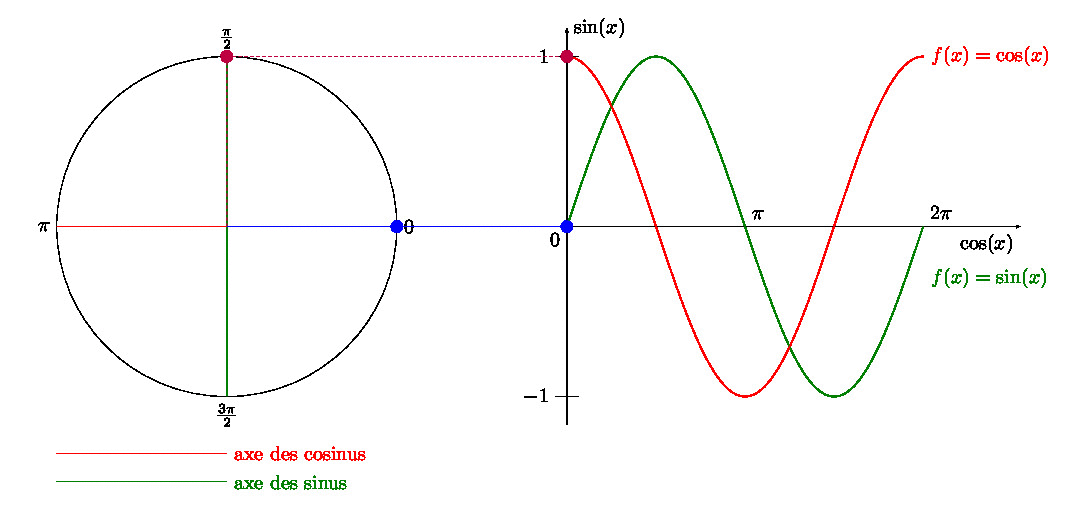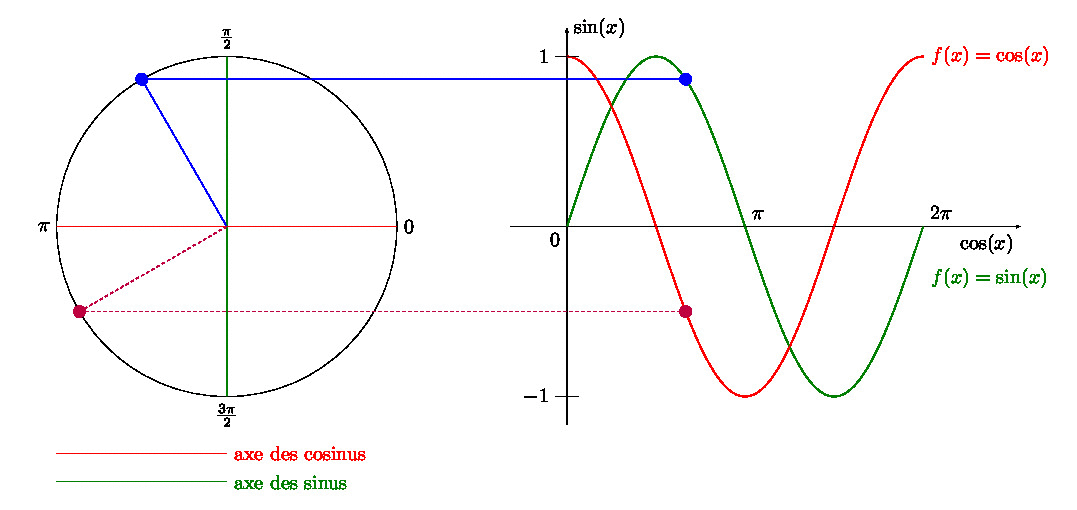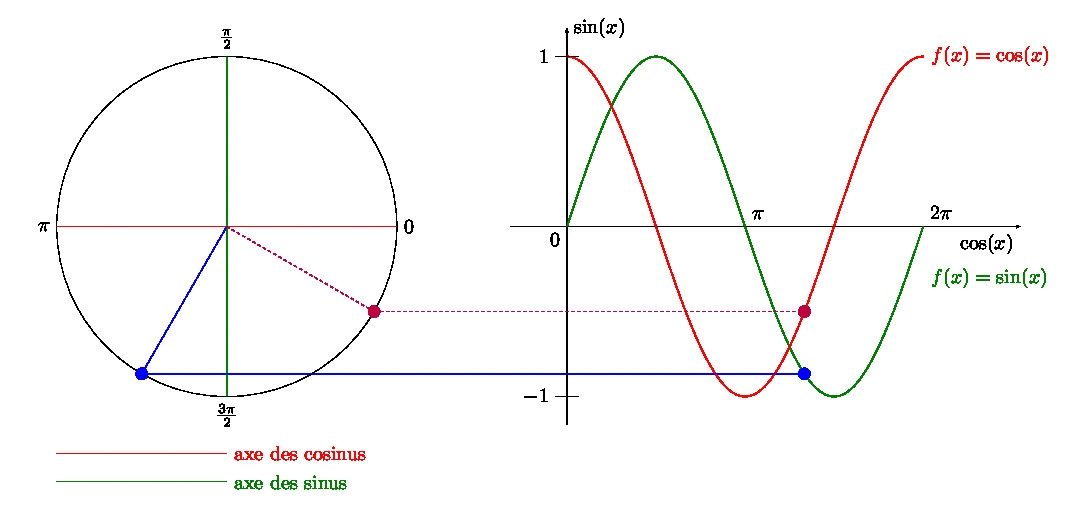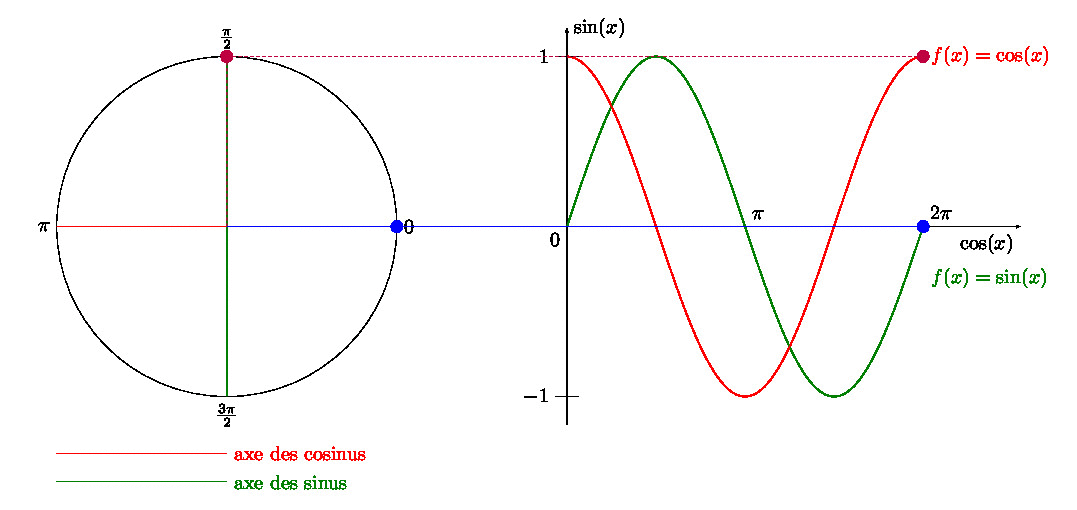
Dans un article précédent, je vous expliquais comment créer un GIF avec \(\LaTeX\), et avec une manipulation Gimp. Trouvant la dernière étape un peu… (comment dire pour rester poli ?) … pénible, je vous propose un combi \(\LaTeX\) + Python + ImageMagick.
(suite…)Si vous avez la curiosité d’aller dans votre cuisine et de prendre une casserole pour en mesurer la hauteur et le rayon de la base, quelle que soit la casserole que vous prendrez, vous verrez que vous obtiendrez la même mesure… Coïncidence ?
(suite…)On considère un polynôme à coefficients entiers : $$P(X)=\sum_{k=0}^n c_kX^k\quad,\quad \forall\; k\in[0;n]\cap\mathbb{N},\ c_k\in\mathbb{Z}.$$L’objectif ici est de démontrer que s’il admet une racine rationnelle irréductible \(\frac{a}{b}\) alors \(a\) divise \(c_0\) et \(b\) divise \(c_ n\).
(suite…)VerbTex, LaTeX sous Android : un des abonnés m’a demandé aujourd’hui s’il était possible de faire du \(\LaTeX\) sous Android. Faisant du \(\LaTeX\) uniquement sur mon PC Windows, je ne m’était jamais posé la question… Mais il y a une solution, et elle est pas dégueu du tout ! Elle s’appelle VerbTeX…
(suite…)L’objectif de cet article est de construire une enveloppe astroïdale en Python avec cette suite de cercles rouges; on va utiliser pour cela le module Turtle. Enveloppe astroïdale en Python : approche mathématique Avant toute chose, il est nécessaire de comprendre comment sont obtenus tous les cercles rouges. Si on Lire la suite…
Cet article est principalement destiné aux élèves de 1ère Math Spécialité.
Parlons dans cet article de mathématiques, et plus précisément du second degré. Alors, vous allez me dire : « oui, mais bon ! C’est super simple, il suffit de connaître les formules et on sait tout faire. » Ce n’est pas totalement faux… mais ce n’est pas suffisant ! Il y a beaucoup de situations qui font intervenir le second degré, notamment ce problème…
(suite…)Cet article est inspiré du post du forum mathematex dont l’adresse est : http://forum.mathematex.net/latex-f6/cadre-pour-algorithme-python-avec-listings-t17255.html
L’idée est ici de créer un environnement « python » (par exemple) qui permet d’écrire un code Python et de le présenter encadré de sorte que le cadre soit ajusté en largeur (ce qui n’est pas le cas par défaut car le cadre tient sur toute la largeur).
(suite…)