Construire le graphe d’une suite avec Python

Comment construire simplement le graphe d’une suite définie par \(u_{n+1}=f(u_n)\) à l’aide Python ?

Mon objectif est de créer un programme Python qui demande à la personne utilisatrice :

• la fonction;
• le premier terme de la suite;
• le nombre de termes à construire;
• la fenêtre \( (x_{\min}) \), \( (x_{\max}) \), \( (y_{\min}) \) et \( (y_{\max}) \);
• le nom sous lequel la figure sera sauvegardée (vide si on ne souhaite pas la sauvegarder).

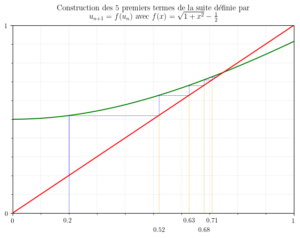
puis de tracer les premiers termes de la suite pour obtenir quelque chose comme ceci:

Graphe d’une suite avec Python: les modules

import numpy as np
import matplotlib.pyplot as plt
from sympy import *
x=Symbol('x')

• Nous aurons besoin du module numpy pour effectuer quelques calculs;
• ensuite, matplotlib nous servira à effectuer les tracés;
• le module sympy nous servira à interpréter la saisie de la fonction comme une fonction. À ce titre, on indique que le symbole de la variable est ‘x’.

Graphe d’une suite avec Python: saisie de la fonction

def definite_function():
    fonction = input("Entrez l'expression de la fonction : ")
    # convertit la chaîne de caractères en 'fonction'
    f = lambdify(x,fonction,'math') # on utilise le module 'math' ici plutôt que 'numpy' car plus pratique
    fonction_latex = input('Syntaxe LaTeX : ')
    return f,fonction_latex

Ici, on demande de saisir d’une part la fonction (avec une syntaxe « classique »), chaîne de caractères que l’on s’empresse tout de suite de transformer en fonction avec la fonction lambdify du module simpy. Puis, on demande la syntaxe \(\LaTeX\) pour que l’affichage du titre soit plus joli. La fonction retourne un couple constitué de la fonction et de la syntaxe « latexienne » de la fonction.

Les autres saisies

def window():
    xmin = float(input('xmin = '))
    xmax = float(input('xmax = '))
    ymin = float(input('ymin = '))
    ymax = float(input('ymax = '))
    return xmin,xmax,ymin,ymax
    
def definite_first_term():
    u = float(input("Entrez le premier terme : "))
    return u

def definite_nb_terms():
    n = int(input('Nombre de termes à construire : '))
    return n

def definite_name():
    name = input("Entrez le nom de l'image à sauvegarder (appuyez sur [Entrée] si vous ne voulez pas sauvegarder l'image) : ")
    return name

Rien de bien compliqué pour ces quelques fonctions qui permettent de saisir le reste des paramètres.

La fonction de construction du graphe

Nous allons la nommer :

def construct_graph(xmin,xmax,ymin,ymax,f,fonction,u,n,name):

et pour commencer, nous allons nommer la figure:

fig = plt.figure()

dans l’objectif de la sauvegarder (éventuellement) plus tard.

Graphe d’une suite: tracé de la grille

Attention: les dernières version de matplotlib font que si on affiche ce qui suit, le graphe de la suite ne s’affiche plus. Je vous conseille donc de ne pas afficher ce qui est dans ce paragraphe. Et honnêtement, il faudrait passer une année entière à étudier matplotlib pour en comprendre le fonctionnement… C’est une vraie usine à gaz !

# tracé du repère et de la grille
    ax = fig.add_subplot(111, aspect='equal')
    ax.grid()
    ax.spines['bottom'].set_position('zero')
    ax.spines['left'].set_position('zero')
    ax.spines['top'].set_visible(False)
    ax.spines['right'].set_visible(False)

Graphe d’une suite: tracé de la courbe

# tracé des courbes
    x = np.linspace(xmin, xmax, 201)
    y = [f(x) for x in [xmin+i*(xmax-xmin)/200 for i in range(201)]]
    plt.plot(x,y,color='green')
    plt.plot(x,x,color='red')

On trace ici la courbe représentative de la fonction f ainsi que la droite d’équation \(y=x\).

Construction des termes

# 1er terme
    x = [u,u]
    y = [0,f(u)]
    plt.plot(x,y,linestyle='--',color='blue',linewidth=0.5)
    # construction des termes
    for i in range(0,n):
        x = [u,u]
        y = [u,f(u)]
        plt.plot(x,y,linestyle='--',color='blue',linewidth=0.5)
        x = [u,f(u)]
        y = [f(u),f(u)]
        plt.plot(x,y,linestyle='--',color='blue',linewidth=0.5)
        if i != n-1:
            x = [f(u),f(u)]
            y = [f(u),0]
            plt.plot(x,y,linestyle='--',color='orange',linewidth=0.5)
        if i%2 == 0:
            yunder=-0.05
        else:
            yunder = -0.1
        plt.text(u-0.02,yunder,np.around(u,2))
        u = f(u)

On fait une boucle dont le nombre d’itérations est égal au nombre de points que l’on veut. Dans un premier temps, on trace en pointillés la ligne verticale qui va de (u,0) à (u,f(u)), dans un deuxième temps, la ligne horizontale qui va de (u,f(u)) à (f(u),f(u)) puis la ligne verticale qui va de (f(u),f(u)) à (f(u),0) pour avoir le terme suivant sur l’axe des abscisses.

Le titre

    params = {'mathtext.default': 'regular' }
    plt.rcParams.update(params)
    plt.rc('text', usetex = True)
    # plt.rc('font', family = 'serif')
    title = "Construction des "+str(n)+" premiers termes de la suite définie par\n$u_{n+1}=f(u_n)$ avec $f(x)="+fonction+"$"
    plt.title(title)
    if name != '':
        fig.savefig(name+'.png',dpi=100,bbox_inches='tight')
    plt.show()

On insère maintenant le titre; les deux premières lignes commentées affichent un titre avec une police de caractères par défaut sous Python (ce qui ne me convient pas, mais qui peut plaire à certaines personnes). Les deux lignes suivantes spécifient que l’on souhaite un affichage \(\LaTeX\).

Fonction principale

if __name__ == '__main__':
    f,fonction = definite_function()
    u = definite_first_term()
    xmin,xmax,ymin,ymax = window()
    n = definite_nb_terms()
    name = definite_name()
    construct_graph(xmin,xmax,ymin,ymax,f,fonction,u,n,name)

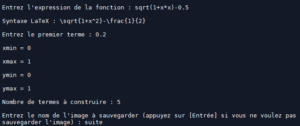
En exécutant ce programme avec les paramètres suivants:

on obtient l’image donnée en préambule de cet article.

Retrouvez le programme complet ci-dessous pour les abonné·e·s: