Voici un problème que les élèves de Terminale pourront comprendre… si la notion de loi uniforme leur dit quelque chose…
Le problème
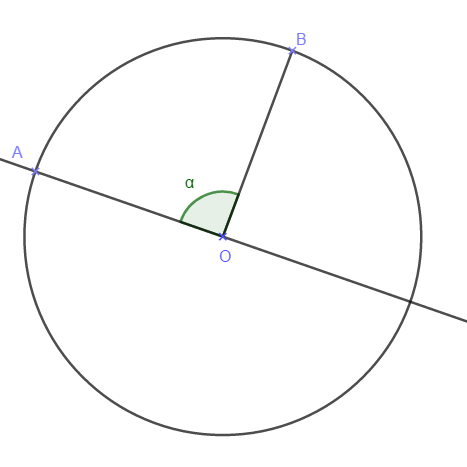
Soient deux points A et B sur un cercle de rayon 1. Quelle est la distance moyenne entre ces deux points ?
Comment commencer ?
Pour vous aider, voici une petite aide: fixons le point A et considérons le diamètre du cercle d’extrémité A. Notons O le centre du cercle. Alors, \(\widehat{AOB}\) est une variable aléatoire continue prenant ses valeurs sur \([0;\pi]\)… et la distance AB s’exprime comme une fonction de cette variable.
Une solution
D’après le théorème d’Al-Kashi,$$AB^2=OA^2+OB^2-2\times OA\times OB\times\cos\alpha$$c’est-à-dire ici (car OA = OB = 1):$$AB^2=2-2\cos\alpha.$$Ainsi,$$AB=\sqrt{2-2\cos\alpha}.$$Or,$$\cos(2x)=1-2\sin^2x$$donc:$$\sin x = \sqrt{\frac{1-\cos(2x)}{2}}.$$En prenant \(x=\frac{\alpha}{2}\), on obtient:$$\sin\frac{\alpha}{2}=\sqrt{\frac{1-\cos\alpha}{2}}= \sqrt{\frac{2-2\cos\alpha}{4}} .$$On déduit alors que:$$AB=2\sin\frac{\alpha}{2}.$$
Le problème étant symétrique par rapport au diamètre passant par A, on peut considérer en effet que l’angle \(\alpha\) est compris entre 0 et \(\pi\). Si on désigne la distance AB par :$$f(\alpha)=2\sin\frac{\alpha}{2}$$alors la distance moyenne est la valeur moyenne de la fonction f:$$\mu=\frac{1}{\pi-0}\int_0^{\pi}f(\alpha)\text{d}\alpha=\frac{2}{\pi}\int_0^{\pi}\sin\frac{\alpha}{2}\text{d}\alpha.$$On a alors:$$\mu=\frac{2}{\pi}\left[-2\cos\frac{\alpha}{2}\right]_0^\pi=\frac{4}{\pi}.$$
La distance moyenne est donc égale à \(\displaystyle\frac{4}{\pi}\), c’est-à-dire environ 1,27.
Remarque sur la variable \(\alpha\)
Nous avons vu que, dans la mesure où B est choisi au hasard, l’angle \(\alpha\) est aléatoire. On peut considérer qu’elle suit la loi uniforme sur \([0;\pi]\). Cela dit, cela n’a aucune importance pour notre problème.
Mais si on se demande quelle est la probabilité que la longueur AB soit plus grande que 1, cela peut nous aider. En effet, $$AB>1 \iff \alpha>\frac{\pi}{3}.$$Si \(\alpha=\frac{\pi}{3}\), le triangle AOB est équilatéral et donc AB=1.
Ainsi,$$P(AB>1)=P\left(\frac{\pi}{3}<\alpha<\pi\right)=\frac{\pi-\frac{\pi}{3}}{\pi-0}=\frac{2}{3}.$$En effet, si X suit la loi uniforme sur [a ; b] alors:$$P(c < X < d)=\frac{d-c}{b-a}.$$