Dans cet article, je fais suite à celui publié hier, et le généralise dans le parallélogramme ci-dessous.
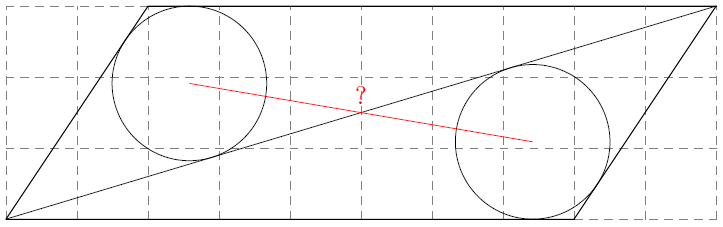
Dans cette figure, les cercles tracés sont tangents aux côtés du parallélogramme et à la diagonale tracée.
Tout est parti du fait que je m’ennuyais en ce dimanche après-midi…
Distance entre les centres des cercles dans le parallélogramme: préliminaires
Il faut avant tout comprendre comment ces cercles ont été tracés.
Un cercle est tangent aux trois côtés du triangle dans lequel il est inscrit si son centre est l’intersection des bissectrices de ce triangle.
Ainsi, le problème se ramène à trouver la position de ces points de concours des bissectrices. Il faut donc, par exemple, déterminer une équation des bissectrices dans un repère donné…
Le repère
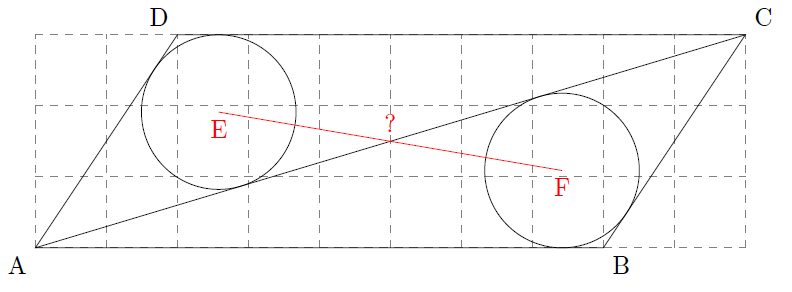
Pour y voir plus clair, on va se placer dans le repère d’origine A, d’axes (AB) et la droite perpendiculaire à (AB) passant par A (non dessinée car peu utile) et d’unité 1 carreau.
\documentclass{standalone}
\usepackage{tikz}
\setlength{\parindent}{0pt}
\begin{document}
\begin{tikzpicture}
\draw[gray,dashed] (0,0) grid (10,3);
\draw (0,0) node[below left] {A} -- (8,0) node[below right] {B} -- (10,3) node[above right] {C} -- (2,3) node[above left] {D} -- cycle;
\draw (0,0)-- (10,3);
\draw (7.41737761672328,1.0886398812302285) circle (1.0886398812302285cm);
\draw (2.58262238327672,1.9113601187697722) circle (1.0886398812302278cm);
\draw [red] (2.58262238327672,1.9113601187697722) node[below] {E} -- (7.41737761672328,1.0886398812302285) node[below] {F} node[midway,above] {?};
\end{tikzpicture}
\end{document}
Le point E
Bissectrice de (AC) et (AD)
Dans ce repère, les équations cartésiennes de (AC) et (AD) sont respectivement:$$(AC)\;:\;-3x+10y=0\qquad;\qquad (AD)\;:\;-\frac{3}{2}x+y=0.$$
La distance de E à (AC) est égale à celle de E à (AD) car E est sur la bissectrice de l’angle formé par ces deux droites, ce qui se traduit par l’égalité:$$\frac{|-3x_E+10y_E|}{\sqrt{(-3)^2+10^2}}=\frac{|-\frac{3}{2}x_E+y_E|}{\sqrt{\left(-\frac{3}{2}\right)^2+1^2}}.$$
On s’appuie ici sur le résultat qui dit que la distance d’un point de coordonnée \((\alpha;\beta)\) à la droite d’équation cartésienne \(ax+by+c=0\) est égale à \( \frac{|a\alpha+b\beta+c|}{\sqrt{a^2+b^2}}\), résultat vu en classe de Terminale (voir de 1ère en exercice pour certain·e·s).
L’égalité précédente donne:$$\sqrt{13}|-3x_E+10y_E|=2\sqrt{109}\left|-\frac{3}{2}x_E+y_E\right|$$c’est-à-dire:$$\begin{array}{ll}-3x_E+10y_E & = \frac{2\sqrt{109}}{\sqrt{13}}\left(-\frac{3}{2}x_E+y_E\right)\\\text{ou}\\ -3x_E+10y_E & = -\frac{2\sqrt{109}}{\sqrt{13}}\left(-\frac{3}{2}x_E+y_E\right)\end{array}$$soit:$$x_E=\frac{11-\sqrt{1417}}{36}y_E \text{ ou } x_E=\frac{11+\sqrt{1417}}{36}y_E.$$
Comme le rapport \(x_E/y_E\) est positif, on retiendra:$$\boxed{x_E=\frac{11+\sqrt{1417}}{36}y_E}$$
Bissectrice de (AC) et (DC)
La droite (DC) a pour équation: \(y=3\). La distance de E à (AD) doit être égale à celle de E à (AD):$$3-y_E=\frac{|-3x_E+10y_E|}{\sqrt{109}}.$$D’où:$$\boxed{x_E=\frac{10+\sqrt{109}}{3}y_E-\sqrt{109}}$$
Des deux égalités encadrées, on déduit:
$$y_E=\frac{36\sqrt{109}}{12\sqrt{109}-\sqrt{1417}+109}\approx1,9.$$
D’où:
$$x_E=\frac{\sqrt{109}(11+\sqrt{1417})}{12\sqrt{109}-\sqrt{1417}+109}\approx2,6.$$
La longueur EF
Bon, là, on va être honnête, on n’a pas super envie de faire la même chose pour le point F car… ben, c’est un peu long hein ? On va invoquer la déesse de la symétrie par rapport au milieu de la diagonale tracée…
Les coordonnées du milieu sont \( I\left( 5;\frac{3}{2} \right) \) donc:$$\begin{align}EF & = 2IE \\ & = 2\sqrt{\big(x_E-x_I \big)^2 + \big(y_E-y_I)^2}\\ & = \frac{\sqrt{ 492728832\sqrt{154453} – 23158255104\sqrt{109} – 6035928192\sqrt{1417} + 288677504448 }}{23544} \\ & \approx 4,9\end{align}$$
J’avoue avoir utilisé Xcas pour la dernière expression…
Conclusion: la prochaine fois que je m’ennuie, je dois absolument arrêter d’inventer des exercices aussi longs… 🙂


