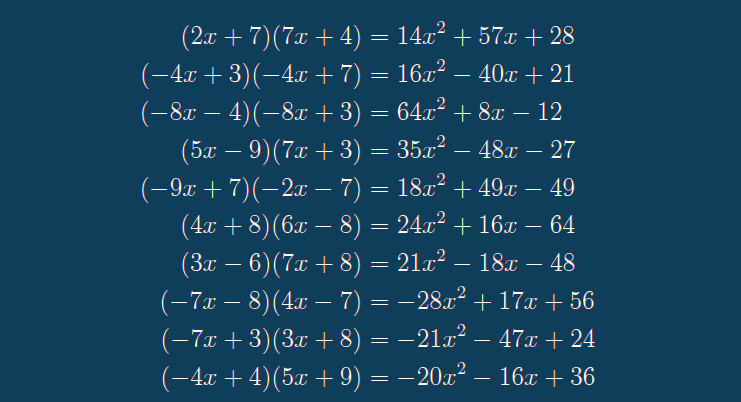Extraire le code \(\LaTeX\) entre deux balises avec Python
5h12 du matin: je n’arrive pas à me rendormir… Je viens d’avoir une idée en tête et comme je ne suis pas procrastinateur, je me lève pour la concrétiser. L’idée du jour (enfin… de la nuit): comment extraire automatiquement la portion de code \(\LaTeX\) contenue entre deux balises \begin{python} et \end{python}, et enregistrer cette portion de code dans un fichier, le tout avec Python ?
(suite…)Créer une arborescence avec Python et LaTeX
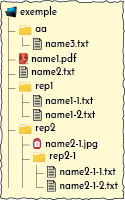
Dans cet article, nous parlerons d’une façon de construire une arborescence en LaTeX à l’aide de Python. Nous allons parler d’arbre informatique pour obtenir un résultat comme celui-ci:
Créer un GIF avec LaTeX, Python et ImageMagick
Créer un GIF avec LaTeX, Python et ImageMagick, comment faire ?
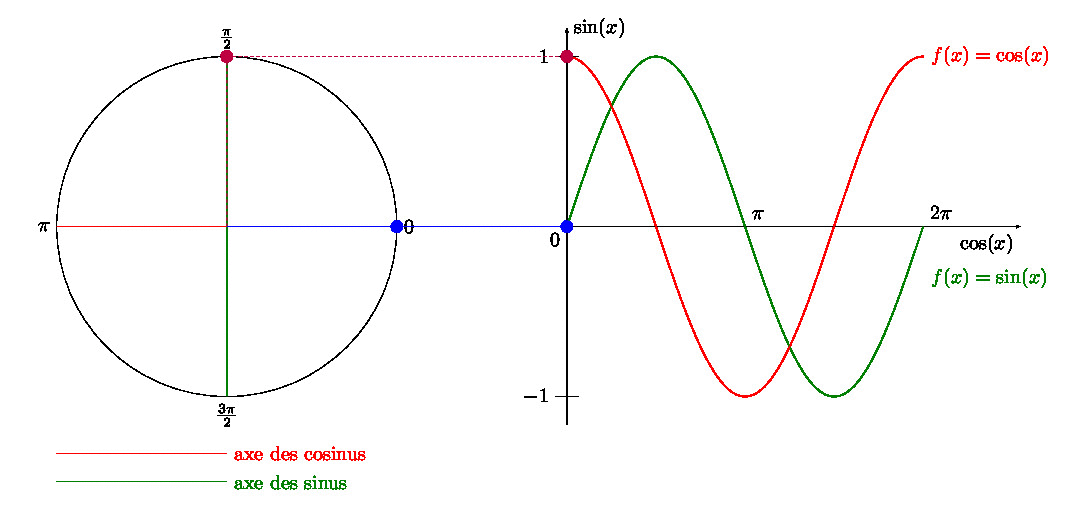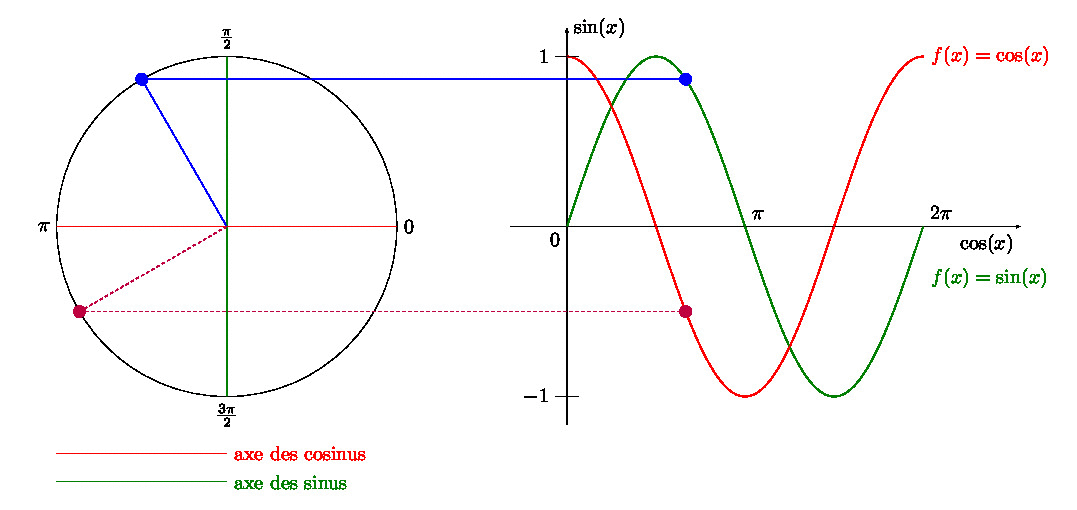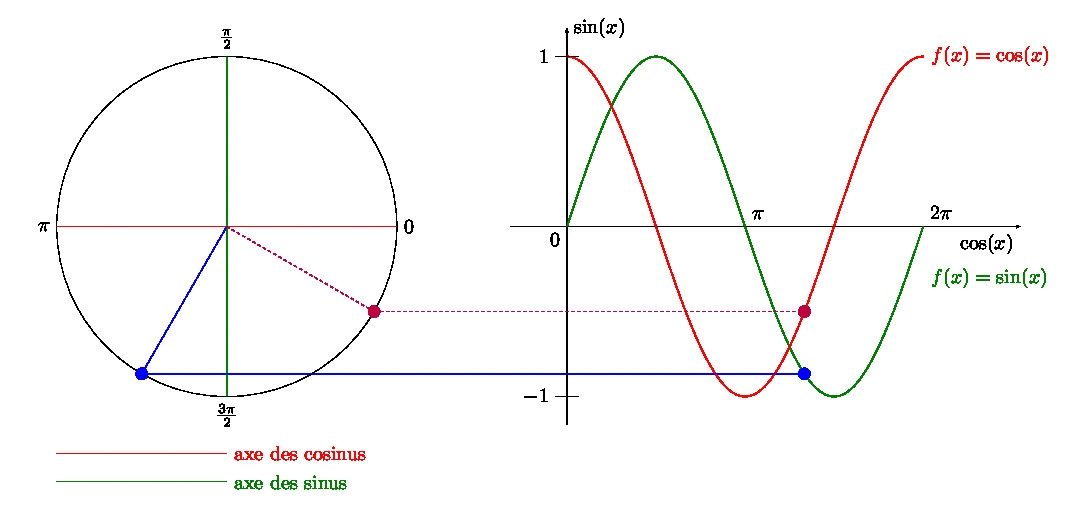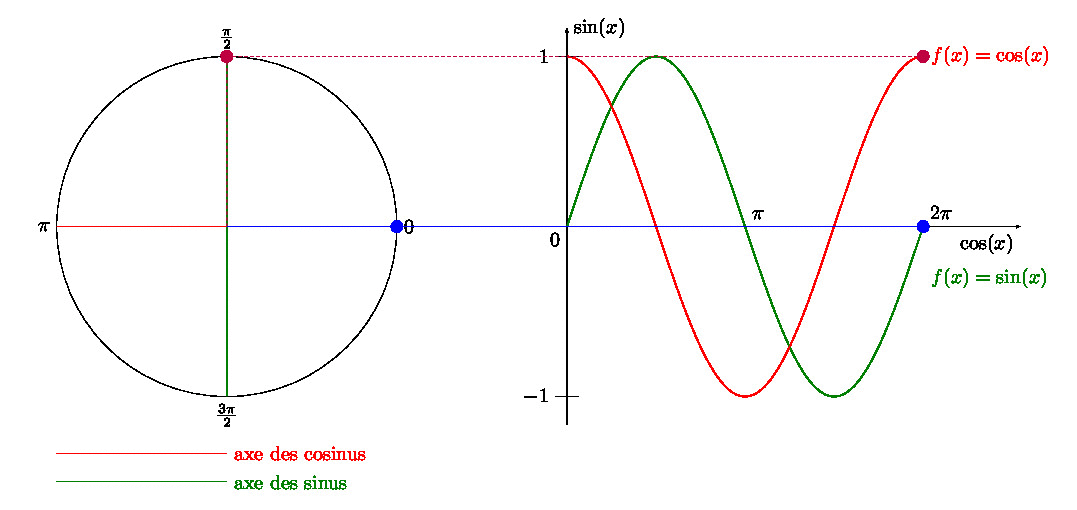
Dans un article précédent, je vous expliquais comment créer un GIF avec \(\LaTeX\), et avec une manipulation Gimp. Trouvant la dernière étape un peu… (comment dire pour rester poli ?) … pénible, je vous propose un combi \(\LaTeX\) + Python + ImageMagick.
(suite…)Décomposition en produit de facteurs premiers sous LaTeX avec Python
La décomposition en produit de facteurs premiers sous LaTeX avec Python semble simple, mais pas tant que ça en définitive… Je voulais en effet créer une commande \(\LaTeX\) acceptant un paramètre (un nombre entier) qui décompose ce dernier en produit de facteurs premiers, et ce à l’aide de Python.
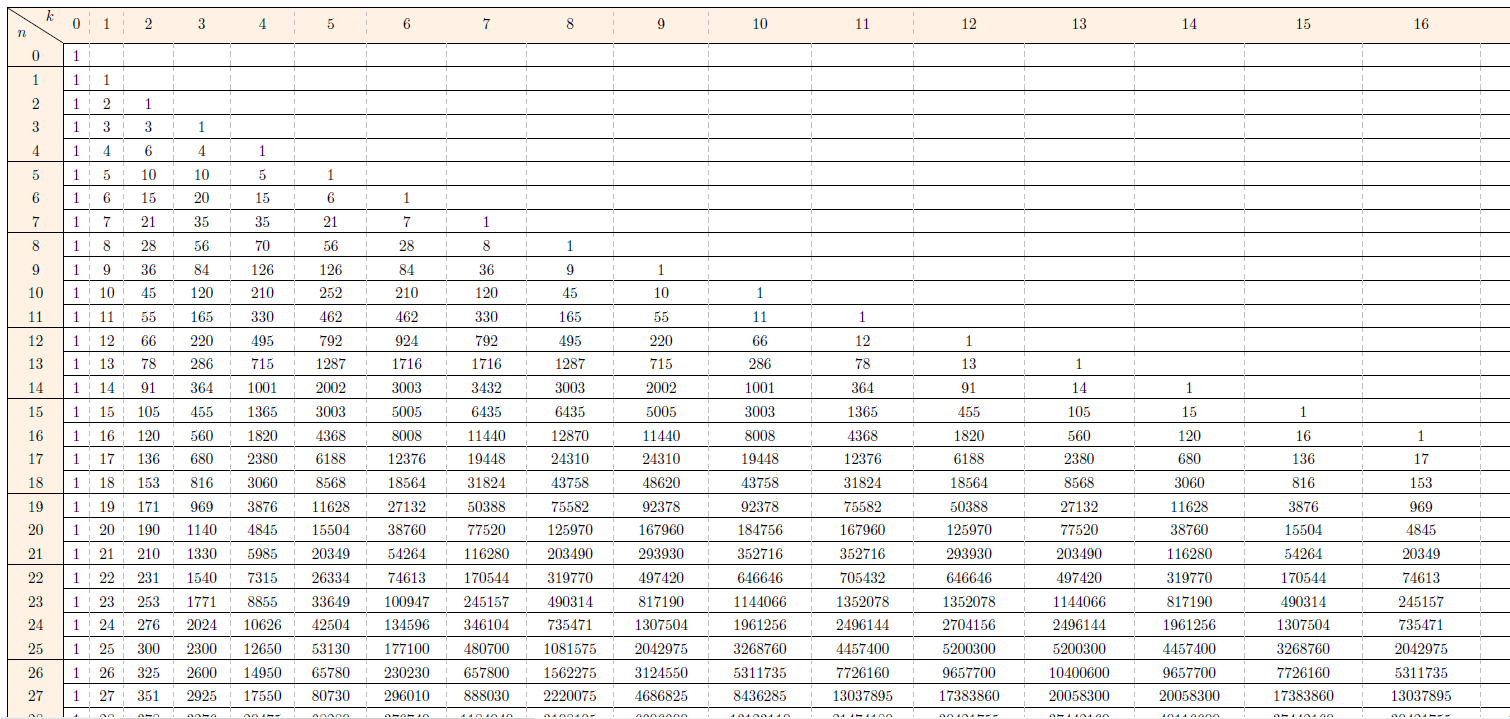
(suite…)Triangle de Pascal construit avec Python et LaTeX
Triangle de Pascal construit avec Python et LaTeX. Nous allons voir dans cet article comment construire le triangle de Pascal en \(\LaTeX\) à l’aide de Python.
(suite…)Créer un fichier LaTeX avec Python
Créer un fichier LaTeX avec Python. Dans un article précédent, je vous expliquais comment, dans un fichier \(\LaTeX\), on pouvait se servir de Python grâce à l’extension Pythontex.
Maintenant, je vais vous expliquer comment faire l’inverse, à savoir comment créer et compiler un fichier \(\LaTeX\) avec un programme Python.
(suite…)Générer des exercices aléatoires en LaTeX avec Python
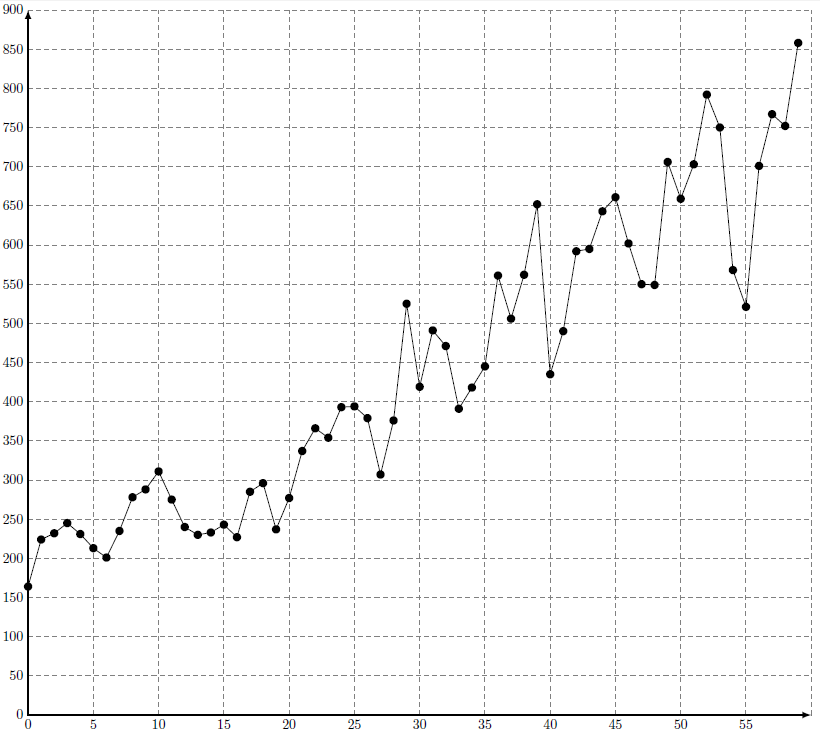
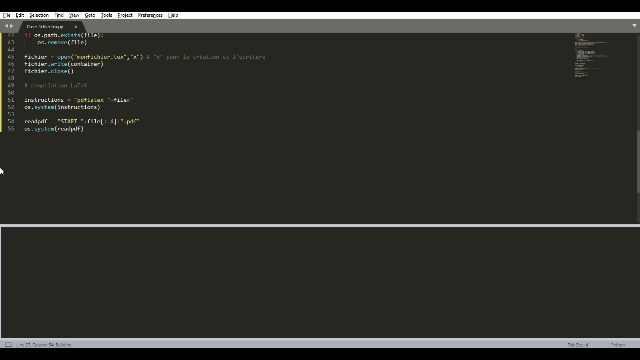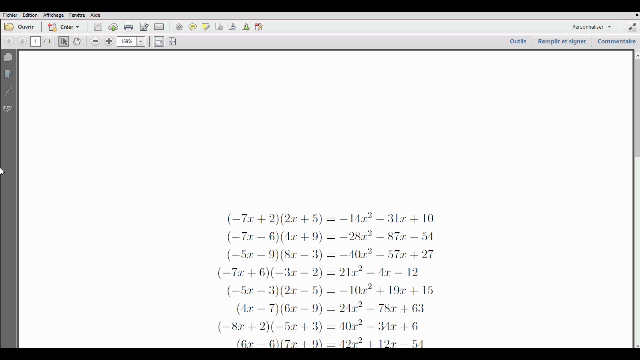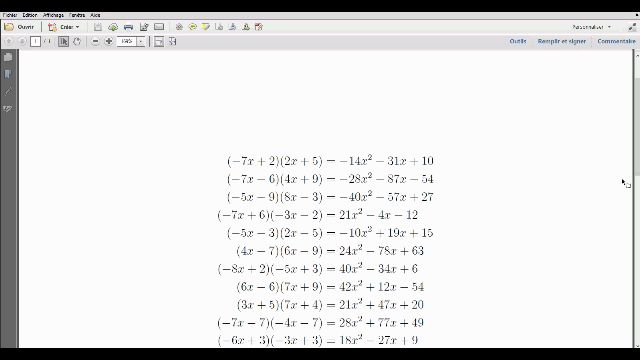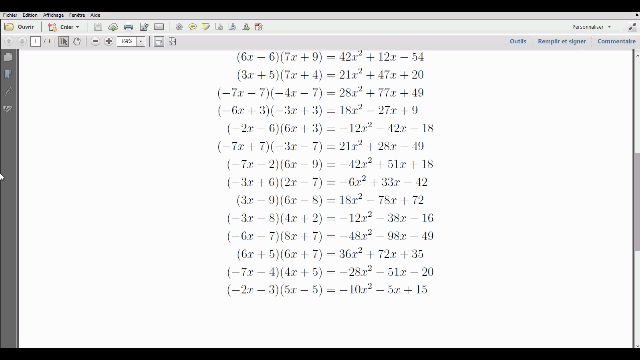
Générer une feuille d’exercices aléatoires avec Python en LaTeX : combien de fois ai-je voulu générer automatiquement des exercices similaires (par exemple, de développement) ? Vous ne le savez pas, mais moi, je le sais : beaucoup trop !
Encore aujourd’hui, j’ai voulu générer une série de multiplications pour faire réviser ses tables une de mes élèves.
Comme je me suis mis à Python il n’y a pas longtemps, et comme dans la foulée je me suis aussi mis à PythonTeX, j’ai forcément pensé à tout ça pour faire ma feuille d’exercices (plutôt que d’inventer et de taper plus de 90 opérations).
Nous allons voir comment.
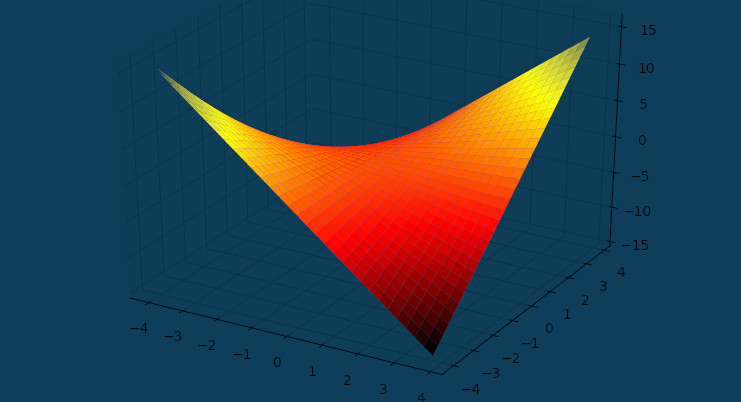
(suite…)Graphiques 3D avec Pythontex sous LaTeX
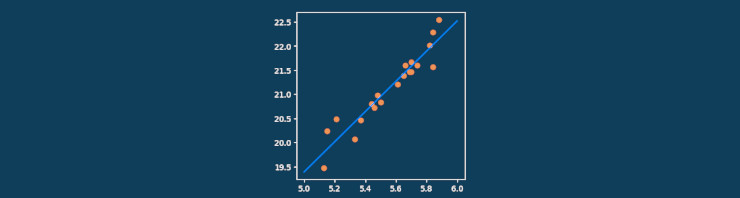
Graphiques 3D et PythonTeX : la prise en main et l’installation de Pythontex peut s’avérer assez fastidieuse quand on s’y met. Par expérience, je peux vous dire que la tâche est encore plus difficile sous Ubuntu quand on est novice (et je le suis !). C’est une des raisons pour lesquelles je n’ai pas souhaité resté sous Ubuntu pour me remettre à Windows.
Une fois Pythontex installé, je pense qu’il est légitime de vouloir l’exploiter à fond, y compris pour faire des choses qu’avec \(\LaTeX\) seul il est difficile de faire. Parmi ces choses,il y a les graphiques, et plus particulièrement les graphiques 3D (car les courbes 2D, PGF sait le faire facilement).
(suite…)