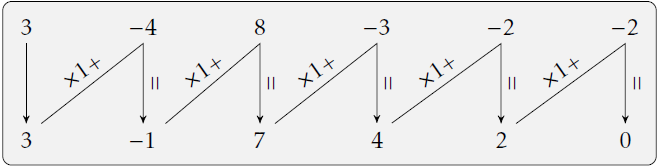
Équation de Bézout en Python
Résoudre une équation de Bézout en Python n’est pas si difficile que ce que l’on pourrait imaginer au premier abord.
Nous allons dans un premier temps faire un rappel sur la manière dont on résout mathématiquement une telle équation, puis nous allons voir une implémentation en Python.
LaTeX et listings en UTF8
LaTeX et listings en UTF8: me concernant, j’encode toujours mes documents \(\LaTeX\) en utf88, et il m’arrive d’utiliser le package listings. Bien entendu, cela provoque quelques soucis. Aussi, lorsque j’ai vu ce topic sur mathemaTeX, et la solution proposé par MB, je me suis dis qu’il serait peut-être intéressant d’approfondir en écrivant cet article.
Fractions continues en Python
Les fractions continues constituent une notion plutôt intéressant en mathématiques. C’est une façon d’écrire les nombres. Dans cet article, je vais expliquer dans les grandes lignes la notion mathématique et dans un second temps, nous allons implémenter en Python une classe permettant de représenter une fraction continue et d’en obtenir sa valeur fractionnaire.
La méthode de Hörner
Considérons un polynôme P, dont une racine est égale à a.
La méthode de Hörner va nous permettre de trouver les coefficients du polynôme Q tel que : \[P(x)=(x-a)Q(x).\]
Bien entendu, il existe d’autres méthodes, comme la division euclidienne de polynômes ou encore la méthode des coefficients indéterminés, mais nous allons voir que la méthode de Hörner a deux avantages sur les autres : sa rapidité et le fait que l’on puisse la programmer aisément.
"Je twitte, donc je suis... ou pas..." (instant philo).
QR code, #HTML et #PHP : pour une fois, je ne vais pas parler de Python... https://www.mathweb.fr/euclide/2020/11/04/qr-code-html-et-php/
Nombres premiers symétriques #maths #Python3 https://www.mathweb.fr/euclide/2020/11/02/nombres-premiers-symetriques/
Nouveau site pour celles et ceux qui cherchent un cours particulier (toutes disciplines) ou qui en propose sur #Bordeaux. Il est entièrement gratuit et conçu par mes soins, donc aucune vente d'adresses électroniques derrière tout ça.
https://cours-particuliers-bordeaux.fr/
#maths Congruences et critère de divisibilité. Pourquoi faire la somme d'un chiffre pour voir s'il est divisible par 3 ? Comment voir si un nombre est divisible par 7 ? Par 11 ? Par 13 ? https://www.mathweb.fr/euclide/2020/10/21/congruences-et-critere-de-divisibilite/