La méthode de Hörner va nous permettre de trouver les coefficients du polynôme Q tel que : \[P(x)=(x-a)Q(x)\] où P est un polynôme dont une racine est égale à a.
Bien entendu, il existe d’autres méthodes, comme la division euclidienne de polynômes ou encore la méthode des coefficients indéterminés, mais nous allons voir que la méthode de Hörner a deux avantages sur les autres : sa rapidité et le fait que l’on puisse la programmer aisément.
Méthode de Hörner: un exemple simple
Considérons le polynôme : \[ P(x)=x^4-3x^3+7x^2-4x-12,\] dont une racine évidente est a = 2.
Nous allons réfléchir à une méthode qui nous permet de trouver les coefficients de Q(x), tel que P(x) = (x – 2)Q(x), à l’aide d’une division euclidienne.
On peut alors remarquer que :
- \(-1 = -3 + 2\times2 \)
- \( 5=7+2\times(-1)\)
- \(6=-4+2\times 5\)
Généralisation
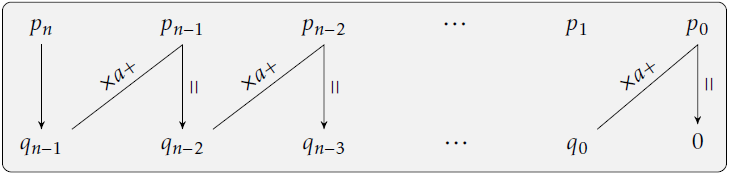
Posons \(P(x)=\displaystyle\sum_{k\leq n} p_kx^k\), \(Q(x)=\displaystyle\sum_{k<n} q_kx^k\) et a une racine de P.
D’après le raisonnement précédent, on peut écrire : \[ \begin{cases} q_{n-1}=p_n\\ q_k=p_{k+1}+aq_{k+1}\quad\forall\ 0\leq k < n\end{cases} \]
Schématisation
Application
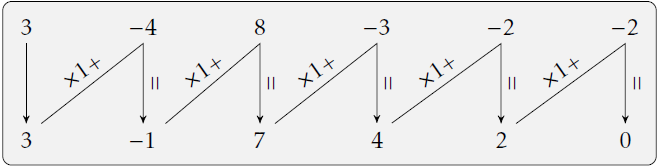
Soit : \[ P(x)=3x^5-4x^4+8x^3-3x^2-2x-2.\] Une racine de P est a = 1, d’où :
D’où : \[ P(x)=(x-1)(3x^4-x^3+7x^2+4x+2). \]
Méthode de Hörner: programme Python
Une implémentation élémentaire
Voici un programme Python qui nécessite très peu de mémoire puisque sa complexité est linéaire.
def horner(r,P):
Q = [ P[0] ]
for k in range( 1 , len(P)-1 ):
Q.append( P[k] + r*Q[k-1] )
return Q
Cela nécessite toutefois quelques explications pour comprendre.
Cette fonction prend pour arguments la racine du polynôme, et la liste des coefficients du polynôme, suivant les puissances décroissantes. Ainsi, pour le polynôme $$P(x)=30x^4-11x^3-219x^2-61x+21$$on pourra écrire:
>>> horner(3,[30,-11,-219,-61,21])
[30, 79, 18, -7]Cela signifie donc que:$$P(x)=(x-3)(30x^3+79x^2+18x-7).$$
Méthode de Hörner en POO
Je vous propose ici de créer une classe Polynome afin d’y insérer une méthode horner(racine):
class Polynome:
def __init__(self,*coefs):
if type(coefs[0]) == tuple:
self.coefs = [ i for i in coefs[0] ]
else:
self.coefs = coefs
self.deg = len( self.coefs ) - 1
def __str__(self):
D = { self.deg-i:self.coefs[i] for i in range( len( self.coefs ) ) }
return str(D)
def horner(self,r):
Q = [ self.coefs[0] ]
for k in range( 1 , len(self.coefs)-1 ):
Q.append( self.coefs[k] + r*Q[k-1] )
return Polynome( tuple(Q) )
Bien sûr, la classe Polynome n’est pas complète, et se concentre uniquement sur ce qui nous intéresse ici. Avec l’exemple du polynôme précédent, cela donne:
>>> P = Polynome(30,-11,-219,-61,21)
>>> print( P.horner(3) )
{3: 30, 2: 79, 1: 18, 0: -7}Cela dit, l’interface graphique est importante… et je ne peux pas laisser cet affichage ainsi! Rectifions donc l’affichage du résultat:
class Polynome:
def __init__(self,*coefs):
if type(coefs[0]) == tuple:
self.coefs = [ i for i in coefs[0] ]
else:
self.coefs = coefs
self.deg = len( self.coefs ) - 1
def __str__(self):
E = { u[0]:"x" + chr(u[1]) for u in ((2,0x00B2), (3,0x00B3), (4,0x2074), (5,0x2075), (6,0x2076), (7,0x2077), (8,0x2078), (9,0x2079)) }
E[0] = ''
E[1] = 'x'
if self.deg > 9:
for d in range( self.deg - 9 ):
E[ 10+d ] = 'x^{'+str(10+d)+'}'
start = True
D = { self.deg-i:self.coefs[i] for i in range( len( self.coefs ) ) }
R = ''
for k,v in D.items():
if v > 0:
if not start:
R += '+'
else:
start = False
if v == 1:
if k != 0:
R += E[k]
else:
R += '1'
else:
R += str(v) + E[k]
elif v < 0:
if v == -1:
if k != 0:
R += '-' + E[k]
else:
R += '-1'
else:
R += str(v) + E[k]
return str(R)
def horner(self,r):
Q = [ self.coefs[0] ]
for k in range( 1 , len(self.coefs)-1 ):
Q.append( self.coefs[k] + r*Q[k-1] )
return Polynome( tuple(Q) )
>>> P = Polynome(1,0,0,0,0,0,0,0,0,1,-1,-1)
>>> print( P.horner(1) )
x^{10}+x⁹+x⁸+x⁷+x⁶+x⁵+x⁴+x³+x²+2x+1L’affichage Unicode des exposants ne va que jusqu’à 9… Nous sommes donc obligés d’afficher les exposants supérieurs à 9 de la manière classique : « x^{…} » (les accolades sont là pour la lisibilité…)
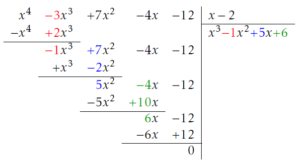



C’est très intéressant dans le sens où l’on donne l’essence de la méthode à partir de la division euclidienne même. De plus la partie programmation avec Python peut aider ceux/celles qui, comme moi ont ce besoin d’illustrer les cours par différents moyens. Merci.