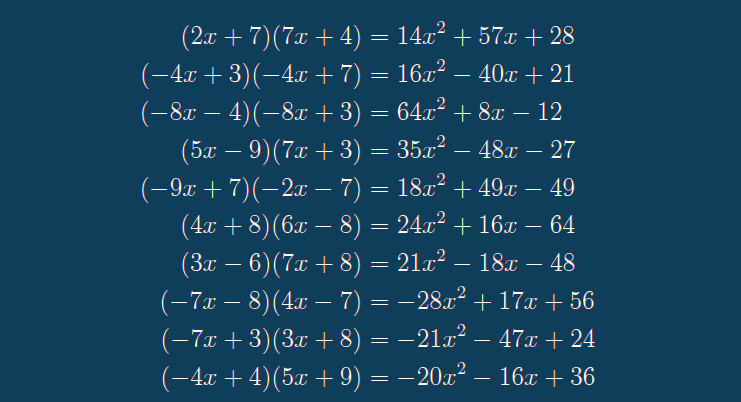Informatique
Décomposition en produit de facteurs premiers sous LaTeX avec Python
La décomposition en produit de facteurs premiers sous LaTeX avec Python semble simple, mais pas tant que ça en définitive… Je voulais en effet créer une commande \(\LaTeX\) acceptant un paramètre (un nombre entier) qui décompose ce dernier en produit de facteurs premiers, et ce à l’aide de Python.
(suite…)
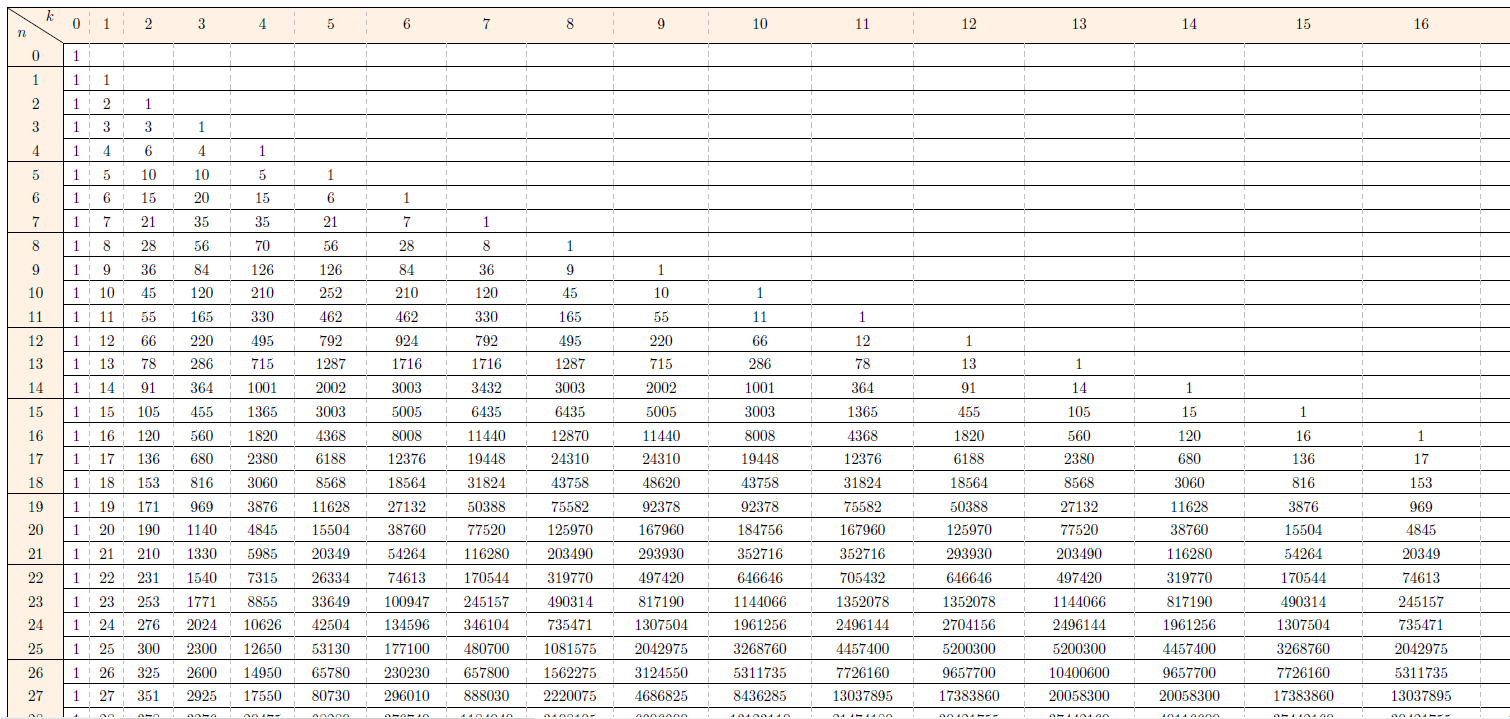
Informatique
Triangle de Pascal construit avec Python et LaTeX
Triangle de Pascal construit avec Python et LaTeX. Nous allons voir dans cet article comment construire le triangle de Pascal en \(\LaTeX\) à l’aide de Python.
(suite…)
Enseignement
Générer des exercices aléatoires en LaTeX avec Python
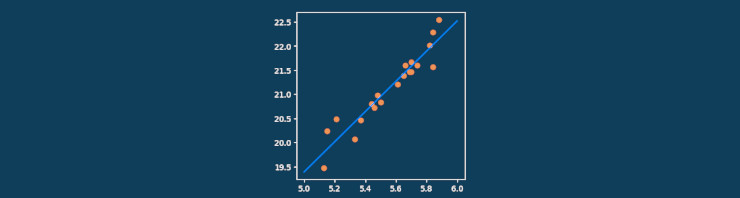
Générer une feuille d’exercices aléatoires avec Python en LaTeX : combien de fois ai-je voulu générer automatiquement des exercices similaires (par exemple, de développement) ? Vous ne le savez pas, mais moi, je le sais : beaucoup trop !
Encore aujourd’hui, j’ai voulu générer une série de multiplications pour faire réviser ses tables une de mes élèves.
Comme je me suis mis à Python il n’y a pas longtemps, et comme dans la foulée je me suis aussi mis à PythonTeX, j’ai forcément pensé à tout ça pour faire ma feuille d’exercices (plutôt que d’inventer et de taper plus de 90 opérations).
Nous allons voir comment.
(suite…)