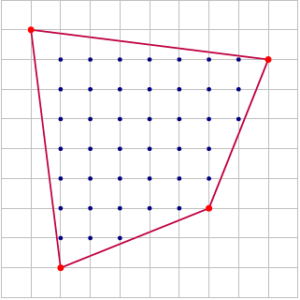
On considère un polygone convexe, c’est-à-dire une figure géométrique constituée de plusieurs côtés rectilignes de sorte qu’aucun sommet ne « rentre » dans la figure, sur un maillage régulier de sorte que chaque sommet soit sur un nœud de ce maillage comme l’illustre le schéma ci-dessous.
Le théorème de Pick stipule que la superficie du polygone peut être calculée de façon simple à l’aide de la formule : \[ \mathcal{A}=i+\frac{b}{2}-1\]
exprimée en unités d’aire, où « i » représente le nombre de nœuds intérieurs au polygone et « b » celui des nœuds se trouvant sur ses côtés.
Par exemple, sur le schéma ci-dessus, i = 41 b = 4 ; d’où : \[ \mathcal{A} = 41+2-1=42. \]
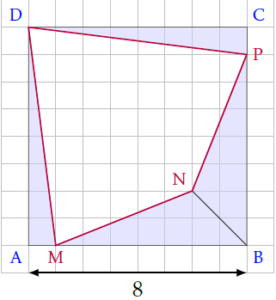
On peut aisément calculer \(\mathcal{A}\) en calculant d’une part l’aire du carré bleu ABCD (voir ci-dessous) et d’autre part, l’aire des triangles AMD, BMN, BNP, et PCD :
- Aire de ABCD : \(8^2=64\);
- Aire de AMD : \(\frac{1}{2}\times1\times8=4\);
- Aire de BMN : \(\frac{1}{2}\times7\times2=7\);
- Aire de BNP : \(\frac{1}{2}\times7\times2=7\);
- Aire de PCD : \(\frac{1}{2}\times1\times8=4\).
Donc l’aire de MDPN est : \[ \mathcal{A}=64-(4+7+7+4)=64-22=42. \]
Démonstration
La formule est-elle vraie pour un rectangle quelconque ?
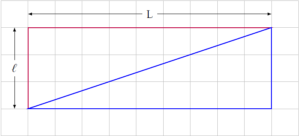
Considérons un rectangle comme ci-dessous :
Ici, \(b=2(\text{L}+1)+2(\ell-1)=2\text{L}+2\ell\) et \(i=(\ell-1)(\text{L}-1)=\text{L}\ell-\text{L}-\ell+1\).
Ainsi, \[ \begin{align*}i+\dfrac{b}{2}-1 & = \text{L}\ell-\text{L}-\ell+1+\frac{2(\text{L}+\ell)}{2}-1\\& = \text{L}\ell\\& = \text{aire du rectangle.}
\end{align*} \]
La formule de Pick est donc vraie pour un rectangle quelconque.
La formule est-elle vraie pour un triangle rectangle ?
Considérons la moitié du rectangle précédent :
Appelons toujours i le nombre de points (nœuds) intérieurs et b = c + d le nombre de points sur le périmètre (c représentant le nombre de points sur les côtés perpendiculaires et d sur l’hypoténuse).
Collons à notre triangle un autre triangle identique (bleu) pour former le rectangle initial. Appelons i’ et b’ les nombres respectifs de points intérieurs au rectangle et sur le périmètre.
On a alors : \[ \begin{cases} i’=2i+d & \text{deux fois le nombre de points intérieurs au triangle,}\\ & \text{plus ceux sur l’hypoténuse.}\\ b’=2c-2 & \text{on enlève deux sommets qui sont en commun.} \end{cases} \]
Or, nous savons que l’aire du triangle est égale à la moitié de celle du rectangle, qui est égale (d’après la section précédente) à \(i’+\frac{b’}{2}-1\).
Donc, l’aire du triangle rectangle est : \[ \begin{align*}\mathcal{A} & = \frac{1}{2}\left(i’+\frac{b’}{2}-1\right)\\ & = \frac{1}{2}\left(2i+d+\frac{2c-2}{2}-1\right)\\ & = \frac{1}{2}\left(2i+d+c-1-1\right)\\ & = i+\frac{b}{2}-1\text{ car }d+c=b. \end{align*} \]
Le théorème de Pick est donc vrai pour le triangle rectangle.
La formule est-elle vraie pour un triangle quelconque ?
Considérons maintenant un rectangle quelconque comme celui représenté ci-dessous :
L’aire du triangle BMP est la différence entre celle du rectangle ABCD et de la somme de celle des triangles rectangles AMB (triangle 1), BCP (triangle 2) et PMD (triangle 3).
Appelons :
- \(i_k\) le nombre de points à l’intérieur du triangle k et \(b_k = c_k+d_k\) le nombre de points sur les bords, avec \(d_k\) représentant le nombre de points sur son hypoténuse (extrémités non comprises) et \(c_k\) représentant le nombre de points sur ces autres côtés, k étant un entier égal à 1, 2 ou 3 ;
- i le nombre de points à l’intérieur du triangle quelconque et \(b=d_1+d_2+d_3+3\) le nombre de points sur ses bords ;
- i’ le nombre de points à l’intérieur du rectangle et b’ le nombre de points sur ses bords.
Notons \(\mathcal{A}\) l’aire du triangle BMP, \(\mathcal{A}_k\) celle du triangle k et \(\mathcal{A}^\prime\) celle du rectangle ABCD. Alors : \[ \begin{align*} \mathcal{A} & = \mathcal{A}^\prime – (\mathcal{A}_1+\mathcal{A}_2+\mathcal{A}_3)\\ & = \left(i’+\frac{b’}{2}-1\right)-\left(i_1+i_2+i_3+\frac{1}{2}(b_1+b_2+b_3)-3\right)\\ & = i’+\frac{b’}{2}-1-\left(i_1+i_2+i_3+\frac{1}{2}(c_1+c_2+c_3+d_1+d_2+d_3) -3\right).\end{align*}\]
Or, \[ i’=i+i_1+i_2+i_3+d_1+d_2+d_3 \] et \[ b’=c_1+c_2+c_3-3, \]
donc : \[ \begin{align*} \mathcal{A} & = i+i_1+i_2+i_3+d_1+d_2+d_3+\frac{c_1+c_2+c_3-3}{2}-1-i_1-i_2-i_3-\frac{c_1+c_2+c_3+d_1+d_2+d_3}{2}+3\\ & = i+\frac{d_1+d_2+d_3+3}{2}-1\\ & = i+\frac{b}{2}-1. \end{align*} \]
Nous avons ainsi démontré que le théorème de Pick était vrai pour un triangle quelconque.
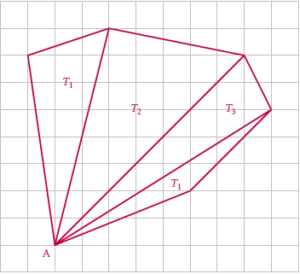
Et maintenant, le polygone convexe !
Un polygone convexe P à n côtés est formé de n-2 triangles, n > 3. Notons \(T_k\) les n-2 triangles qui constituent le polygone. Je vais ici prendre un hexagone pour avoir un appui visuel :
Je conviens alors de découper P à partir d’un même point A et en nommant les triangles de gauche à droite \(T_1,\ T_2,\ \ldots,\ T_{n-2}\).
Je note alors :
- \(c_1\) le nombre de points sur les deux côtés de \(T_1\) qui coïncident avec deux côtés de P ;
- \(c_{n-2}\) le nombre de points sur les deux côtés de \(T_{n-2}\) qui coïncident avec deux côtés de P ;
- \(c_k\), \(1\leq k \leq n-3\), le nombre de points sur le seul côté de \(T_k\) qui coïncide avec un côté de P ;
- \(d_k\), \(1\leq k \leq n-3\), le nombre de points sur le côté de \(T_k\) intérieur à P qui ne coïncide pas avec un côté de \(T_{k-1}\) ;
- \(i_k\) le nombre de points intérieurs à \(T_k\) ;
- i le nombre de points intérieurs à P ;
- b le nombre de points sur les bords de P.
On a alors : \[ i=\sum_{k=1}^{n-2} i_k+\sum_{k=1}^{n-3} d_k \] et \[ b=c_1+(c_2-1)+(c_3-1)+\cdots+(c_{n-3}-1)+(c_{n-2}-2)\;, \]
soit : \[ b=\sum_{k=1}^{n-2} c_k -(n-2)\;,\]
ou encore : \[ b=\sum_{k=1}^{n-2}c_k-n+2.\]
En notant \(\mathcal{A}\) l’aire de P et \(\mathcal{A}_k\) celle de \(T_k\), on a : \[ \begin{align*}\mathcal{A} & = \sum_{k=1}^{n-2}\mathcal{A}_k\\ & = \mathcal{A}_1+ \sum_{k=2}^{n-3}\mathcal{A}_k+\mathcal{A}_{n-2}\\ & = i_1+\frac{b_1}{2}-1+\sum_{k=2}^{n-3}\mathcal{A}_k+i_{n-2}+\frac{b_{n-2}}{2}-1\\ & = i_1+i_{n-2}+\frac{b_1+b_{n-2}}{2}-2+\sum_{k=2}^{n-3}\left(i_k+\frac{b_k}{2}-1\right)\\
& = i_1+i_{n-2}+\frac{b_1+b_{n-2}}{2}-2+\sum_{k=2}^{n-3}\left( i_k+\frac{d_{k-1}+c_k+d_k+1}{2}-1\right)\\ & = i_1+i_{n-2}+\frac{b_1+b_{n-2}}{2}-2+\sum_{k=2}^{n-3}i_k + \frac{1}{2}\sum_{k=2}^{n-3}c_k + \frac{1}{2}\sum_{k=2}^{n-3}(d_{k-1}+d_k)\\&\qquad -\frac{1}{2}(n-4) \\ & = \sum_{k=1}^{n-2}i_k+\frac{c_1+d_1+c_{n-2}+d_{n-3}}{2}+\frac{1}{2}\sum_{k=2}^{n-3}c_k+\frac{1}{2}\sum_{k=2}^{n-3}(d_{k-1}+d_k)\\&\qquad-\frac{1}{2}n\\ & = \sum_{k=1}^{n-2}i_k+\frac{1}{2}\sum_{k=1}^{n-2}c_k + \sum_{k=1}^{n-2}d_k-\frac{1}{2}n\\ & = \left(\sum_{k=1}^{n-2}i_k+\sum_{k=1}^{n-3}d_k\right)+\frac{1}{2}\sum_{k=1}^{n-2}c_k-\frac{1}{2}n\\ & = i+\frac{b+n-2}{2}-\frac{1}{2}n\\
& = i+\frac{b}{2}-1. \end{align*} \]
Le théorème de Pick est donc démontré pour tout polygone convexe.
Télécharger cet article au format PDF : Théorème de Pick
Obtenir les sources \(\LaTeX\) du document PDF :




Bonjour,
Quelques commentaires à propos de l’article, qui donne de quoi avoir une démonstration complète.
En effet, la démonstration en quatre étapes nécessite quelques compléments (dans le même style). Par exemple, le rectangle n’est pas quelconque, ses côtés sont parallèles au quadrillage, idem pour le triangle rectangle, ses côtés de l’angle droit sont aussi parallèles au quadrillage (pas grave mais ça mériterait une remarque dans la preuve).
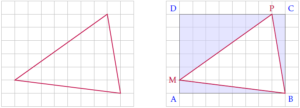
En revanche, le découpage du rectangle pour le triangle quelconque ne suffit pas. Que faire si on a un triangle obtus comme le triangle MNP de la deuxième image d’ouverture ? Ça rendrait la preuve moins sympathique puisqu’il faudrait traquer tous les cas possibles et leur étude serait fastidieuse.
On peut remarquer que le théorème de Pick est valable même si le polygone est concave, si ses côtés ne se chevauchent pas, comme ça arrive avec le faux parallélogramme croisé (et ça marche aussi avec des trous qui ne se chevauchent pas, avec la même réserve mais en comptant en plus le nombre de trous).