Cet article a pour objectifs de construire trois cercles tangents de rayons différents et de calculer l’aire du domaine compris entre ces trois cercles.

Construction

Rappelons que deux cercles tangents sont deux cercles qui se coupent en un unique point. Ainsi, trois cercles \(\mathcal{C}_1,\ \mathcal{C}_2\) et \(\mathcal{C}_3\) tangents sont tels que \(\mathcal{C}_i\cap\mathcal{C}_j=\{M_i\}\), avec \(i\neq j\), i = 1, 2 ou 3 et j = 1, 2 ou 3.

Notons respectivement \(r_i\) et \(O_i\)  le rayon et le centre de \(\mathcal{C}_i\), i = 1, 2 ou 3.

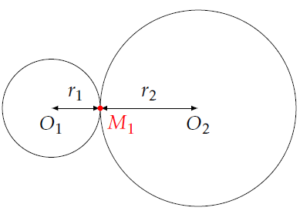
Construire \(\mathcal{C}_1\) et \(\mathcal{C}_2\) est aisé : il suffit de tracer le segment \([O_1O_2]\) de longueur \(r_1+r_2\).Nous cherchons donc à construire \(\mathcal{C}_3\), de rayon \(r_3\) de sorte qu’il soit tangent aux deux cercles. On doit alors avoir \(O_1O_3=r_1+r_3\) et \(O_2O_3=r_2+r_3\).

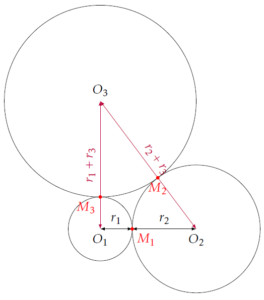
On peut ainsi construire le cercle de centre \(O_1\) et de rayon \(r_1+r_3\), puis le cercle de centre \(O_2\) de rayon \(r_2+r_3\). Ces deux cercles sont sécants en un point qui est \(O_3\).

Pour construire \(\mathcal{C}_3\), il suffit de tracer le cercle de centre \(O_3\) passant par le point d’intersection de \([O_1O_3]\) et de \(\mathcal{C}_1\) (par exemple).

Aire du domaine entre les trois cercles

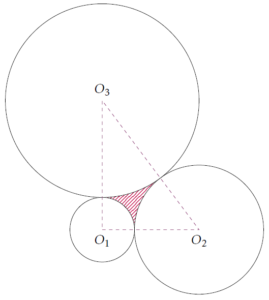
Ce qui nous intéresse est l’aire du domaine hachuré représenté ci-dessous :

Théoriquement, son aire est obtenue en soustrayant à l’aire du triangle \(O_1O_2O_3\) la somme des aires des secteurs angulaires de centres \(O_1,\ O_2\) et \(O_3\).

À ce stade, nous ne connaissons que \(O_1O_2,\ O_2O_3\) et \(O_1O_3\).

À l’aide de la formule de Héron, on peut déterminer l’aire du triangle \(O_1O_2O_3\) et à l’aide de la formule d’Al-Kashi, nous pouvons trouver la mesure des angles \(\widehat{O_2O_1O_3},\ \widehat{O_1O_3O_2}\) et \(\widehat{O_3O_2O_1}\).

Aire de \(O_1O_2O_3\)

\(\mathcal{A}_T=\sqrt{p(p-a)(p-b)(p-c)}\), avec \(a=O_1O_2,\ b=O_2O_3,\ c=O_3O_1,\ p=\frac{1}{2}(a+b+c)\).

Aire du secteur angulaire de centre \(O_1\)

Je note \(\alpha_1=\widehat{O_1}\) dans le triangle \(O_1O_2O_3\).

Avec les notations précédentes, on a : \[ b^2=a^2+c^2-2ac\cos\alpha_1\;, \]

soit : \[ \alpha_1=\arccos\left(\frac{a^2+c^2-b^2}{2ac}\right). \]

Ainsi, l’aire du secteur angulaire correspondant est égale à : \[ \mathcal{A}_1=\frac{1}{2}\alpha_1r_1^2=\frac{1}{2}\arccos\left(\frac{a^2+c^2-b^2}{2ac}\right)r_1^2. \]

(Je conviens ici d’exprimer les angles en radians)

Aire des secteurs angulaires de centres \(O_2\) et \(O_3\)

En notant \(\alpha_2=\widehat{O_2}\) et \(\alpha_3=\widehat{O_3}\) dans le triangle \(O_1O_2O_3\), et en utilisant ce que nous venons de faire précédemment, on a : \[\alpha_2=\arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)\qquad\text{et}\qquad\alpha_3=\arccos\left(\frac{b^2+c^2-a^2}{2bc}\right).\]

Ainsi, l’aire des secteurs angulaires correspondant respectivement à \(\alpha_2\) et \(\alpha_3\) sont égales à : \[ \mathcal{A}_2=\frac{1}{2}\arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)r_2^2\quad\text{et}\quad\mathcal{A}_3=\frac{1}{2}\arccos\left(\frac{b^2+c^2-a^2}{2bc}\right)r_3^2. \]

Aire du secteur hachuré

\[ \begin{align*} \begin{split} \mathcal{A} & = \mathcal{A}_T-\mathcal{A}_1-\mathcal{A}_2-\mathcal{A}_3\\ & = \sqrt{p(p-a)(p-b)(p-c)}-\frac{1}{2}\left[\arccos\left(\frac{a^2+c^2-b^2}{2ac}\right)r_1^2\right.\\ & \left.+\arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)r_2^2+\arccos\left(\frac{b^2+c^2-a^2}{2bc}\right)r_3^2\right]. \end{split}\end{align*} \]

Application

Sur le schéma fait en début de section 3, j’ai pris \(r_k=k\) cm. On a alors : \[ \begin{align*} a&=1+2=3\\ b&=2+3=5\\ c&=1+3=4\\p&=\frac{1}{2} (3+5+4)=6\end{align*}\]

ce qui donne : \[ \begin{align*} \mathcal{A}&=\sqrt{6\times3\times1\times2}-\frac{1}{2}\left(1^2\times\arccos\frac{9+16-25}{2\times3\times4}\right.\\ & \left.\qquad+2^2\times\arccos\frac{9+25-16}{2\times3\times5}+3^2\times\arccos\frac{25+16-9}{2\times5\times4}\right)\\ \mathcal{A}& = 6-\frac{1}{2}\left(\arccos 0+4\arccos\frac{3}{5}+9\arccos\frac{4}{5}\right)\\ \mathcal{A} & \approx 0,464~\text{cm}^2. \end{align*} \]

Obtenir le fichier source \(\LaTeX\) du document PDF: