Marche aléatoire en Python: c’est le thème d’un exercices que j’ai vu dans un livre de spécialité Math niveau 1ère. Il concerne la marche aléatoire d’une puce dans un plan rapporté à un repère orthonormé.
Marche aléatoire en Python: le contexte
Une puce part de l’origine du repère et effectue 10 pas de façon aléatoire : à chaque pas, elle peut avancer ou reculer en abscisses ou en ordonnées. Voici un exemple de cette marche:
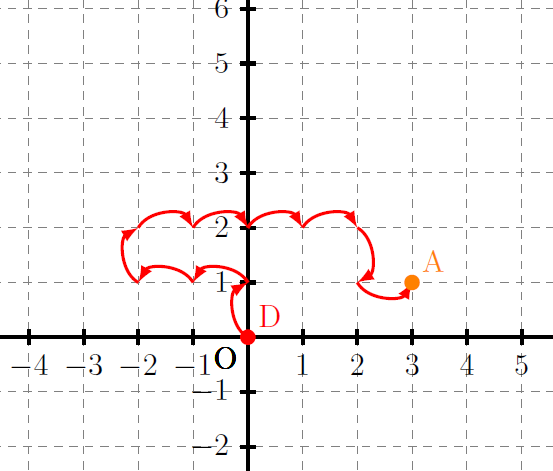
On s’intéresse à la probabilité de revenir à l’origine du repère à la fin de la marche. Pour cela, on va utiliser un programme Python…
Marche aléatoire: le programme Python
Une fonction qui simule une marche aléatoire en Python
Commençons en effet par implémenter une fonction qui a pour mission de retourner les coordonnées du point d’arrivée à l’issue de la marche:
# Python < 3.10
from random import randint
def marche(n):
x, y = 0, 0
for i in range(n):
b = randint(0,3)
if b == 0:
x += 1
elif b == 1:
x -= 1
elif b == 2:
y += 1
else:
y -= 1
return (x,y)
# Python 3.10+
from random import randint
def marche(n):
x, y = 0, 0
for i in range(n):
match randint(0,3):
case 0: x += 1
case 1: x -= 1
case 2: y += 1
case 3: y -= 1
return (x,y)
On commence par importer la fonction randint(a,b) qui choisit aléatoirement un nombre entier entre a et b (compris), car nous avons besoin de cette fonction dans celle que nous allons écrire.
Remarque : encore une fois (oui, je ragote), inutile d’importer TOUTES les fonctions de random… Donc évitez le « from random import * » ou pire encore : « import random ».
Une fonction qui calcule une fréquence
Maintenant, implémentons une fonction cible(x,y,n) qui retournera la fréquence de fois où l’on est arrivé à l’origine à la fin de la marche sur les n marches effectuées.
def cible(x,y,n):
c = 0 # compteur de fois où l'on atteint (0,0) à l'issue d'une marche
for i in range(n):
if marche(10) == (x,y):
c += 1
return c / n
Maintenant, regardons ce que cela donne avec n = 1000:
print( cible(0,0,1000) )
J’obtiens 0,081. Comme je suis de nature sceptique (comme la fosse), je décide de faire 20 simulations:
for i in range(20):
print( cible(0,0,1000) )
Et là, j’obtiens:
0.042 0.058 0.053 0.066 0.058 0.059 0.055 0.059 0.063 0.062 0.058 0.06 0.062 0.075 0.05 0.051 0.056 0.068 0.053 0.048
La première valeur était donc une valeur peut représentative au final… Ces probabilités fluctuent autour de 0,0625 qui n’est autre que \(0,25^2\). Essayons d’expliquer cela…
Étude mathématique d’une marche aléatoire
Simplifions un peu…
Plutôt que de prendre 10 pas pour une marche, choisissons-en 2, et ce pour pouvoir facilement représenter cette expérience aléatoire à l’aide d’un arbre:
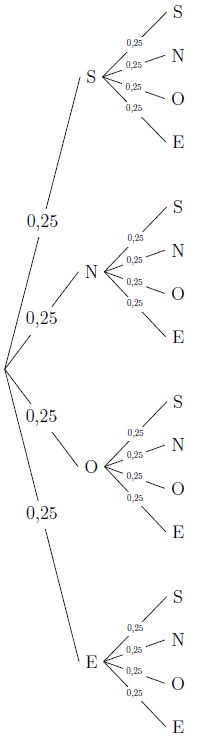
Première remarque : notre arbre comporte 4² = 16 issues. Ensuite, nous avons autant de chance d’aller vers le Nord, le Sud, l’Est ou l’Ouest, à savoir 1 chance sur 4. Ainsi, la probabilité d’obtenir le chemin « X-Y », où \((X;Y)\in\{S;N;O;E\}^2\) est égale à 0,25², soit 0,0625.
La probabilité de revenir à l’origine est la probabilité d’avoir les chemins : « SN », « NS », « EO » ou « OE », soit égale à \(4\times\frac{1}{4^2}=\frac{1}{4}\).
Une marche à 4 pas…
Tentons maintenant de regarder ce qui se passe si on fait 4 pas (en effet, si on n’en fait que 3, il est impossible de revenir à l’origine).
Notre arbre compterait \(4^4 = 256\) issues (inutile de vous dire que je ne vais pas m’amuser à le tracer!), et chaque chemins menant à une issue aurait une probabilité égale à \(0,25^4\).
Les chemins qui font que l’on se retrouve à l’origine à la fin de la marche sont: NNSS, SSNN, NSNS, SNSN puis OOEE, EEOO, OEOE, EOEO, et puis NSEO, SNEO, NSOE, SNOE, OENS, OESN, EONS et EOSN, soit 4².
Ainsi, la probabilité de revenir à l’origine est égale à \(4^2 \times \frac{1}{4^4}=\frac{1}{4^2}\). Hum… Intéressant ! On trouve la même probabilité que pour une marche à 2 pas… Je dis ça, je dis rien…
Une marche à 10 pas
L’arbre contient \(4^{10}\) issues et chaque issue à la même probabilité d’être obtenue, à savoir \(\frac{1}{4^{10}}\). De plus, les chemins qui mènent à l’origine du repère doivent comporter autant de « N » que de « S » et autant de « O » que de « E ». C’est ici que ça se complique car il faut dénombrer toutes les possibilités.
Avec aucun « N »
Il doit alors y avoir cinq « O » et cinq « E ». On cherche le nombre d’anagrammes de « OOOOOEEEEE », qui est:$$\frac{10!}{5!^2}=252.$$
Avec un « N »
Il y a alors un « S », quatre « O » et quatre « E ». Notre recherche correspond à la recherche du nombre d’anagrammes de « SNOOOOEEEE », égal à:$$\frac{10!}{4!^2}=6300.$$
Avec deux « N »
On cherche le nombre d’anagrammes de « NNSSOOOEEE », qui est:$$\frac{10!}{2!^2\times3!^2}=25200.$$
Avec k « N », \(0 \leq k \leq 5\)
D’après ce qui vient d’être vu, on peut aisément conclure que le nombre de chemins comportant k « N » (et donc k « S », 5-k « O » et 5-k « E ») est:$$\frac{10!}{(k!(5-k)!)^2}.$$ On peut aussi raisonner autrement en disant qu’il faut placer k « N » parmi les 10 emplacements possibles, puis placer k « S » parmi les 5-k emplacements restants, puis placer 5-k « O » parmi les 10-2k emplacements restants, et enfin placer les 5-k « E » parmi les 5-k emplacements restants, ce qui donne \(\displaystyle\binom{10}{k}\times\binom{10-k}{k}\times\binom{10-2k}{5-k}\times\binom{5-k}{5-k}\) possibilités, qui est égal au résultat précédent (heureusement!).
En ajoutant tous les résultats, on trouve 63504 chemins possibles. Et si vous n’êtes pas convaincus, vous pouvez toujours, avec Python, vous en assurer avec ce programme:
L = ['O','E','N','S']
P = []
for a in L:
for b in L:
for c in L:
for d in L:
for e in L:
for f in L:
for g in L:
for h in L:
for i in L:
for j in L:
P.append([a,b,c,d,e,f,g,h,i,j])
n = 0
for e in P:
if e.count('O') == e.count('E') and e.count('N') == e.count('S'):
n += 1
print(n)
Mais personnellement, j’ai utilisé Xcas pour obtenir ce même résultat avec le code suivant:
n:=0;for(k=0;k<=5;k++){n:=n+factorial(10)/((factorial(k)*factorial(5-k))^2);}
La probabilité de revenir à l’origine du repère est donc égale à \(\frac{63504}{4^{10}}\approx0,060562\). Ben sur le coup, je me suis bien planté! Je pensais obtenir une probabilité exactement égale à \(\frac{1}{16}\) mais ce n’est a priori pas le cas (même si on n’en est pas loin).
Comme quoi, il faut se méfier des intuitions… surtout quand on sait qu’elles sont très souvent mauvaises !



Bonjour, je n’arrive pas à comprendre pourquoi vous dites que la probabilité du nombre de fois où pour une marche à 4 pas je reviens à l’origine est égal à la probabilité d’une marche à 2 pas ( pour une marche à 2 pas la probabilité est de 0,25 et pour une marche à 4 pas elle est de 0,0625)
Aussi que peut on en conclure avec le nombre que l’on trouve à la fin par rapport à celui que l’on trouve grâce au programme python)
Une dernière question, si on fait une fréquence sur 1000 pas plûtot que 10 c’est pour que cette fréquence devienne une probabilité c’est ça ?)
Tout est expliqué dans l’article, je ne peux rien dire de plus concernant la première partie de la question (tout est démontré).
Concernant la deuxième partie, je ne la comprends pas: « Aussi que peut on en conclure avec le nombre que l’on trouve à la fin par rapport à celui que l’on trouve grâce au programme python) « …
Enfin, si on simule un grand nombre de fois, c’est parce que la loi des grands nombres (théorème mathématique vu en terminale) stipule que la fréquence se rapproche de la probabilité quand le nombre de simulation tend vers l’infini.
Enfaite ce que je n’arrive pas à comprendre c’est le lien entre le résultat que l’on trouve avec python ( avec 1000 pas on a environ une probabilité de 0,0625 de revenir à l’origine ) et le résultat que l’on trouve mathématiquement en calculant quel est la probabilité de revenir à l’origine du repère a l’issu d’une marche aléatoire de 10 pas .( Résultats sensiblement les mêmes )
Quand on fait une simulation informatique avec un grand nombre, c’est justement pour avoir une valeur approchée de la probabilité. Là, on peut calculer mathématiquement la probabilité, mais dans les cas les plus compliqués, la simulation permet d’avoir une idée de la probabilité.