Nous allons voir comment construire le graphique d’une suite avec Python et LaTeX, notamment avec TiKZ, une solution graphique de LaTeX.
Introduction pour construire le graphique d’une suite avec Python et LaTeX
J’avais déjà parlé de cela sur la page https://www.mathweb.fr/euclide/2019/05/21/construire-le-graphe-dune-suite-avec-python/, mais il s’agissait (dans ce dernier article) de construire le graphe directement en Python avec matplotlib.
Les plus averti·e·s d’entre vous, qui utilisent \(\LaTeX\), pourraient avoir envie de construire ce graphe directement avec TiKZ.
Une solution serait d’utiliser pythontex, mais très peu pratique.
Personnellement, je préfère générer le fichier \(\LaTeX\) en Python.
Comment construire le graphique d’une suite en LaTeX à l’aide de Python ?
Dans un premier temps, il faut se mettre d’accord sur la forme de la suite: nous allons considérer une suite \((u_n)\) définie par son premier terme \(u_0\) et par la relation de récurrence \(u_{n+1}=f(u_n)\).
Un premier exemple de graphique d’une suite avec LaTeX et Python
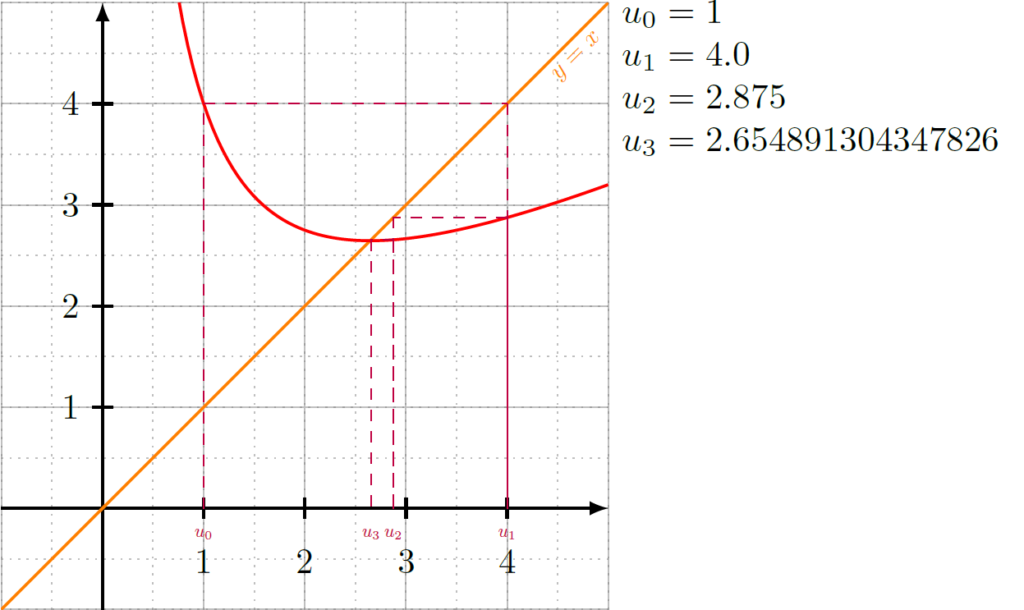
Je considère la suite définie par \(u_0=1\) et \(u_{n+1}=\frac{1}{2}\left(u_n+\frac{7}{u_n}\right)\). J’ai ainsi la fonction \(f(x)=\dfrac{1}{2}\left(x+\frac{7}{x}\right)\).
Avec le programme que j’ai écrit en Python, quand je tape:
>>> G = Graphique_suite( fonction = '0.5*(x+7/x)', \
n = 4 , \
u0 = 1, \
xmin = -1, \
xmax = 5, \
ymin = -1,\
ymax = 5, \
stepgrid = 0.5)
>>> G.exportPdf('essai' , values = True)j’obtiens le PDF suivant:
et le fichier \(\LaTeX\) suivant:
\documentclass{standalone}
\usepackage{tikz}
\begin{document}
\begin{tikzpicture}[baseline=4.8cm]
\draw[dotted,gray,opacity=0.5] (-1,-1) grid[step=0.5] (5,5);
\draw[gray,opacity=0.5] (-1,-1) grid (5,5);
\draw[thick,->,>=latex] (-1,0) -- (5,0);
\draw[thick,->,>=latex] (0,-1) -- (0,5);
\clip (-1,-1) rectangle (5,5);
\draw[thick,orange] plot[domain=-1:5] (\x,\x) node[below left,rotate=45,scale=0.7,outer xsep=3mm] {$y=x$};
\draw[thick,red] plot[domain=0.1:5,samples=100] (\x,{0.5*(\x+7/\x)});
% Graduation des axes
\draw[thick] (1,0.1) -- (1,-0.1) node[below,outer sep=2mm] {1};
\draw[thick] (2,0.1) -- (2,-0.1) node[below,outer sep=2mm] {2};
\draw[thick] (3,0.1) -- (3,-0.1) node[below,outer sep=2mm] {3};
\draw[thick] (4,0.1) -- (4,-0.1) node[below,outer sep=2mm] {4};
\draw[thick] (0.1,1) -- (-0.1,1) node[left] {1};
\draw[thick] (0.1,2) -- (-0.1,2) node[left] {2};
\draw[thick] (0.1,3) -- (-0.1,3) node[left] {3};
\draw[thick] (0.1,4) -- (-0.1,4) node[left] {4};
\draw[dashed,purple] (1,0) node[below,scale=0.5,outer ysep=3mm] {$u_{0}$} -- (1,4.0);
\draw[dashed,purple] (1,4.0) -- (4.0,4.0);
\draw[dashed,purple] (4.0,4.0) -- (4.0,0);
\draw[dashed,purple] (4.0,0) node[below,scale=0.5,outer ysep=3mm] {$u_{1}$} -- (4.0,2.875);
\draw[dashed,purple] (4.0,2.875) -- (2.875,2.875);
\draw[dashed,purple] (2.875,2.875) -- (2.875,0);
\draw[dashed,purple] (2.875,0) node[below,scale=0.5,outer ysep=3mm] {$u_{2}$} -- (2.875,2.654891304347826);
\draw[dashed,purple] (2.875,2.654891304347826) -- (2.654891304347826,2.654891304347826);
\draw[dashed,purple] (2.654891304347826,2.654891304347826) -- (2.654891304347826,0);
\node[below,scale=0.5,outer ysep=3mm,purple] at (2.654891304347826,0) {$u_{3}$};
%
\end{tikzpicture}
\begin{minipage}[t]{40mm}
$u_{0} = 1$\\
$u_{1} = 4.0$\\
$u_{2} = 2.875$\\
$u_{3} = 2.654891304347826$\\
\end{minipage}
\end{document}
La classe Python pour construire le graphique d’une suite
Comme vous pouvez le constater sur l’exemple précédent, on crée un objet « Graphique_suite » avec les instances suivantes:
- fonction : chaîne de caractères définissant la fonction;
- n : entier désignant le nombre de termes à placer sur le graphe;
- u0 : la valeur du premier terme de la suite;
- xmin et xmax désignent les bornes de l’intervalle sur lequel tracer le graphique;
- ymin et ymax désignent les bornes de l’intervalle image souhaité;
- stepgrid : par défaut, cette valeur vaut 0.2; cela correspond aux pointillés de la grille en gris;
- xscale : l’échelle en abscisse (pour agrandir ou réduire le graphique)
- yscale : l’échelle en ordonnée
- valwidth : largeur (en millimètres) de la boîte contenant les valeurs des termes successifs de la suite
- Df = [ x , y ] : domaine de définition de la courbe à tracer.
Un autre exemple
>>> G = Graphique_suite( fonction = 'sqrt(x)', \
n = 7 , \
u0 = 0.1, \
xmin = -0.2, \
xmax = 1.2, \
ymin = -0.2,\
ymax = 1.2, \
stepgrid = 0.1, \
xscale = 10, \
yscale = 6,\
valwidth = 50, \
Df = [0,1.2])
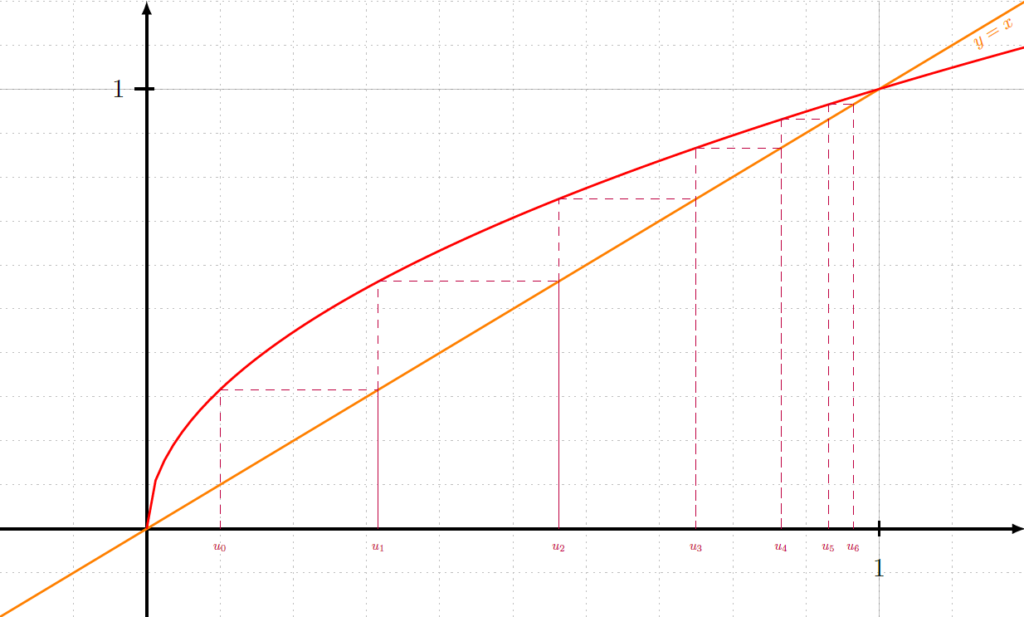
>>> G.exportPdf('essai' , values = False)Un autre exemple
>>> G = Graphique_suite( fonction = 'ln(x+3)', \
n = 4 , \
u0 = -1, \
xmin = -3, \
xmax = 3, \
ymin = -2,\
ymax = 3, \
stepgrid = 0.2, \
xscale = 2, \
yscale = 2,\
valwidth = 50, \
Df = [-2.8,3])
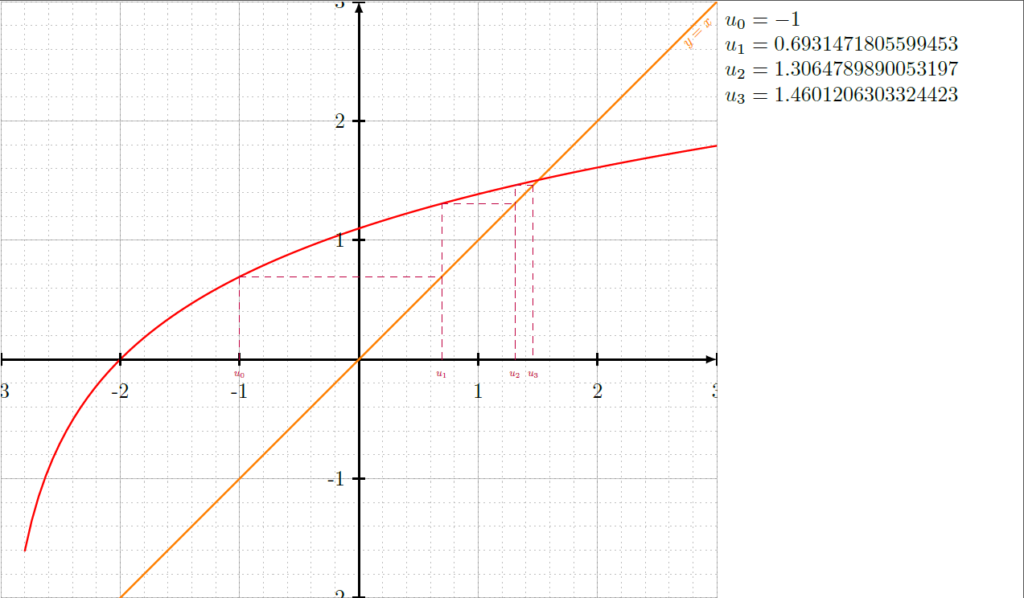
>>> G.exportPdf('essai' , values = True)La classe Python
# Classe Graphique_suite
# Author: Stéphane Pasquet
# Date : 2022-05-07
# URL : https://mathweb.fr
from sympy import Symbol, lambdify
from os import system, remove
from os.path import exists
from math import atan, pi
class Graphique_suite:
def __init__(self,fonction,n,u0,xmin,xmax,ymin,ymax,stepgrid=0.2,xscale=1,yscale=1,valwidth=40,Df=None):
self.fonction = fonction
x = Symbol('x')
self.f = lambdify(x,self.fonction,'math')
self.xmin = xmin
self.xmax = xmax
self.ymin = ymin
self.ymax = ymax
self.stepgrid = stepgrid
self.xscale = xscale
self.yscale = yscale
self.valwidth = valwidth
if Df == None:
self.Df = [ xmin , xmax ]
else:
self.Df = Df
self.u0 = u0
self.n = n
self.U = [ (0,self.u0) ] # self.U = liste des termes successifs (k,u(k))
for k in range(1,self.n):
self.U.append( ( k , self.f(self.U[k-1][1]) ) )
def graphique_tex(self,values):
tex = '\\documentclass{standalone}\n'
tex += '\\usepackage{tikz}\n'
tex += '\\begin{document}\n'
tex += '\\begin{tikzpicture}[baseline='+str((self.ymax-0.2)*self.yscale)+'cm,xscale='+str(self.xscale)+',yscale='+str(self.yscale)+']\n'
tex += f'\\draw[dotted,gray,opacity=0.5] ({self.xmin},{self.ymin}) grid[step={self.stepgrid}] ({self.xmax},{self.ymax});\n'
tex += f'\\draw[gray,opacity=0.5] ({self.xmin},{self.ymin}) grid ({self.xmax},{self.ymax});\n'
tex += f'\\draw[thick,->,>=latex] ({self.xmin},0) -- ({self.xmax},0);\n'
tex += f'\\draw[thick,->,>=latex] (0,{self.ymin}) -- (0,{self.ymax});\n'
tex += f'\\clip ({self.xmin},{self.ymin}) rectangle ({self.xmax},{self.ymax});\n'
tex += f'\\draw[thick,orange] plot[domain={self.xmin}:{self.xmax}] '
tex += '(\\x,\\x) node[below left,rotate='+str(180*atan(self.yscale/self.xscale)/pi)+',scale=0.7,outer xsep=3mm] {$y=x$};\n'
tex += '\\draw[thick,red] plot[domain='+str(self.Df[0])+':'+str(self.Df[1])+',samples=100] (\\x,{'+self.fonction.replace('x','\\x')+'});\n'
tex += '% Graduation des axes\n'
for a in range(int(self.xmin),int(self.xmax)+1):
if a != 0:
tex += f'\\draw[thick] ({a},0.1/{self.yscale}) -- ({a},-0.1/{self.yscale}) node[below,outer sep=2mm] '
tex += '{' + str(a) + '};\n'
for a in range(int(self.ymin),int(self.ymax)+1):
if a != 0:
tex += f'\\draw[thick] (0.1/{self.xscale},{a}) -- (-0.1/{self.yscale},{a}) node[left] '
tex += '{' + str(a) + '};\n'
for k in range(self.n-1):
tex += f"\\draw[dashed,purple] ({self.U[k][1]},0) node[below,scale=0.5,outer ysep=3mm] " + '{$u_{'+str(k)+'}$} -- '
tex += f"({self.U[k][1]},{self.U[k+1][1]});\n"
tex += f"\\draw[dashed,purple] ({self.U[k][1]},{self.U[k+1][1]}) -- ({self.U[k+1][1]},{self.U[k+1][1]});\n"
tex += f"\\draw[dashed,purple] ({self.U[k+1][1]},{self.U[k+1][1]}) -- ({self.U[k+1][1]},0);\n"
tex += f"\\node[below,scale=0.5,outer ysep=3mm,purple] at ({self.U[k+1][1]},0) "
tex += '{$u_{'+str(self.n-1)+'}$};\n%\n'
tex += '\\end{tikzpicture}\n'
if values:
tex += '\\begin{minipage}[t]{'+str(self.valwidth)+'mm}\n'
for v in self.U:
tex += '$u_{'+ str(v[0]) + '} = ' + str(v[1]) + '$\\\\\n'
tex += '\\end{minipage}\n'
tex += '\\end{document}'
return tex
def exportPdf(self,name,values=False):
if exists(f'{name}.tex'):
remove(f'{name}.tex')
fichier = open(f"{name}.tex","x")
fichier.write(self.graphique_tex(values))
fichier.close()
system(f"pdflatex {name}.tex")
system(f"START {name}.pdf")