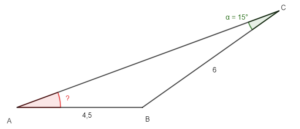
Trouver la mesure d’un angle dans un triangle
Cet exercice, qui consiste à trouver la mesure d’un angle dans un triangle où l’on connait la mesure de deux côtés et celle d’un autre angle, a été proposé lors d’un test à des élève suisses, dont le niveau équivaut à celui de 1ère en France.