Trouver une aire
Le problème est le suivant : trouver l’aire du domaine représenté en bleu sur la figure ci-dessous:
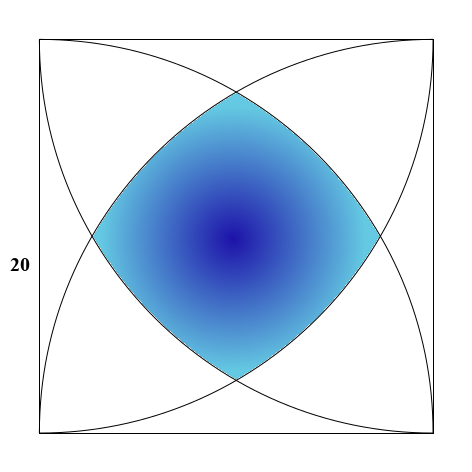
Le problème est le suivant : trouver l’aire du domaine représenté en bleu sur la figure ci-dessous:

Je suis tombé sur une vidéo dans laquelle on demande de résoudre l’équation:$$4^x+6^x=9^x$$ d’inconnue réelle \(x\). Cette équation, au demeurant compliquée, n’est en définitive pas si compliquée à résoudre que ça… mais comme toujours en mathématiques, tout dépend de l’intuition que l’on a face à un problème jamais rencontré.
(suite…)Sam Loyd (1841 – 1911) est ce que je pourrais appeler un \ »récréateur de problèmes mathématiques » : il a créé des problèmes mathématiques se voulant récréatifs.
Vous connaissez le jeu du taquin ? Et bien, c’est Sam Loyd qui popularisa ce jeu.
En voici quelques uns que je trouve intéressants.
(suite…)Les équations polynomiales de degré 3 sont de la forme : \[ ax^3+bx^2+cx+d=0.\qquad(1) \]
Ce dont nous pouvons être assuré.e.s, c’est qu’elle admet au moins une solution réelle. En effet, la fonction : \[ f(x)=ax^3+bx^2+cx+d\]
est continue sur \(\mathbb{R}\) et, de plus, \[ \left\{ \begin{array}{l} \lim\limits_{x\to-\infty} f(x)=\lim\limits_{x\to-\infty} (ax^3)=\text{sgn}(-a)\infty\\\lim\limits_{x\to+\infty} f(x)=\lim\limits_{x\to+\infty} (ax^3)=\text{sgn}(a)\infty\end{array}\right.\]
où \(\text{sgn}(a)\) désigne le signe de a.
Ainsi, d’après le théorème des valeurs intermédiaires, l’équation \(f(x)=0\) admet au moins une solution sur \(\mathbb{R}\).
(suite…)