Longueur d’une bissectrice dans un triangle: considérons un triangle quelconque ABC ; posons alors AB = c, AC = b et BC = a.
Posons \(\ell\) la longueur de la bissectrice issue de C ; alors, on a:
Démontrons ce résultat…
Longueur d’une bissectrice dans un triangle: démonstration (niveau : 1ère)
L’aire du triangle:
- ABC est donnée par la formule : \[ \mathcal{A}_{\text{ABC}}=\frac{1}{2}ab\sin(2\alpha). \]
- riangle ACI est donnée par la formule : \[ \mathcal{A}_{\text{ACI}}=\frac{1}{2}b\ell\sin(\alpha). \]
- BCI est donnée par la formule : \[ \mathcal{A}_{\text{BCI}}=\frac{1}{2}a\ell\sin(\alpha). \]
On en déduit alors : \[ \begin{align*} & \mathcal{A}_{\text{ABC}} = \mathcal{A}_{\text{ACI}}+\mathcal{A}_{\text{BCI}}\\ \Leftrightarrow\ & \frac{1}{2}ab\sin(2\alpha) = \frac{1}{2}b\ell\sin(\alpha) + \frac{1}{2}a\ell\sin(\alpha)\\ \Leftrightarrow\ & ab\sin(2\alpha) =\ell\sin(\alpha)(b + a)\\ \Leftrightarrow\ & \ell = \frac{ab}{a+b}\times\frac{\sin(2\alpha)}{\sin\alpha}. \end{align*}\]
Or, \[ \sin(2\alpha)=2\sin\alpha\cos\alpha.\]
D’où : \[\ell = \frac{ab}{a+b}\times\frac{2\sin\alpha\cos\alpha}{\sin\alpha},\]
et donc : \[\ell = \frac{ab}{a+b}\times 2\cos\alpha.\]
On en déduit alors que : \[ \ell^2 = \frac{(ab)^2}{(a+b)^2}\times 4\cos^2\alpha.\]
Or, \[ \cos^2\alpha = \frac{1+\cos(2\alpha)}{2},\]
d’où : \[ \begin{align*} \ell^2 & = \frac{(ab)^2}{(a+b)^2}\times 4\times\frac{1+\cos(2\alpha)}{2}\\ & = \frac{(ab)^2}{(a+b)^2}\times 2(1+\cos(2\alpha)) \end{align*} \]
La relation d’Al-Kashi dans le triangle ABC donne : \[ c^2=a^2+b^2-2ab\cos(2\alpha).\]
Donc : \[ \cos(2\alpha)=\frac{a^2+b^2-c^2}{2ab}.\]
On a alors : \[ \begin{align*} \ell^2 & = \frac{(ab)^2}{(a+b)^2}\times 2\left(1+\frac{a^2+b^2-c^2}{2ab}\right)\\ & = \frac{(ab)^2}{(a+b)^2}\times 2\left(\frac{2ab+a^2+b^2-c^2}{2ab}\right)\\ & = \frac{ab}{(a+b)^2}(a^2+2ab+b^2-c^2)\\ & = \frac{ab}{(a+b)^2}\left[(a+b)^2-c^2\right]\\ & = ab\left(1-\frac{c^2}{(a+b)^2}\right) \end{align*} \]
On en déduit alors (car \(\ell\geq 0\)): \[ \ell=\sqrt{ab\left(1-\frac{c^2}{(a+b)^2}\right)}.\]
Les sources \(\LaTeX\) du document PDF
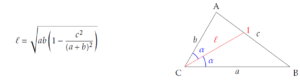



C’est cool ça nous aide beaucoup dans nos exercices