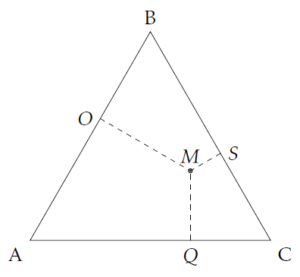
Le théorème de Viviani stipule que : « dans un triangle équilatéral, la somme des distances d’un point intérieur quelconque aux trois côtés est constante. »
Autrement dit, quelle que soit la position du point M dans le triangle ABC, \[ \text{MS}+\text{MQ}+\text{MO} = \text{constante}.\]
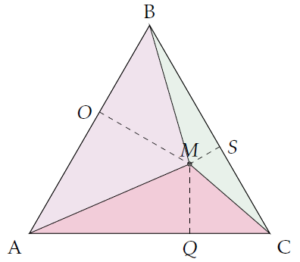
Démonstration du théorème de Viviani avec les aires
Posons \(A_1\) l’aire du triangle ABM ; alors, \[ A_1=\frac{1}{2}\text{AB}\times\text{MO}.\]
Posons \(A_2\) l’aire du triangle ACM ; alors, \[ A_2=\frac{1}{2}\text{AC}\times\text{MQ}.\]
Posons \(A_3\) l’aire du triangle CBM ; alors, \[ A_3=\frac{1}{2}\text{BC}\times\text{MS}.\]
Posons \(A_0\) l’aire du triangle ABC ; alors, \[ A_0=\frac{1}{2}\text{AC}\times h\]
où h est la hauteur de ABC issue de B. À l’aide du théorème de Pythagore, on peut démontrer que : \[ h = \frac{\sqrt{3}}{2}\text{AC}.\]
On en déduit que : \[ A_0=\frac{\sqrt{3}}{4}\text{AC}^2.\]
Or, \[ A_0=A_1+A_2+A_3\] et\[ \text{AC} = \text{AB} = \text{BC}. \]
Donc : \[ \frac{\sqrt{3}}{4}\text{AC}^2=\frac{1}{2}\text{AC}\left(\text{MO}+\text{MS}+\text{MQ}\right) \]
soit : \[ \text{MO}+\text{MS}+\text{MQ} = \frac{\sqrt{3}}{2}\text{AC}.\]
On voit alors que la somme des 3 distances ne dépend pas de la position de M.
Démonstration avec l’analyse
On rapporte le plan au repère \(\left(\text{A}~;\vec{\text{AC}},\vec{j}\right)\), où \(\vec{\text{AC}}\cdot\vec{j}=0\) et \(\|\vec{\text{AC}}\|=\|\vec{j}\|\). Alors, \[ \text{A}(0~;0)\quad ;\quad \text{C}(1~;0)\quad ;\quad \text{B}\left(\frac{1}{2}~;\frac{\sqrt{3}}{2}\right).\]
Ainsi, \[ \vec{\text{AB}}\left(\begin{array}{c}\frac{1}{2}\\ \frac{\sqrt{3}}{2}\end{array}\right),\]
d’où : \[ (\text{AB})\;:\; \frac{\sqrt{3}}{2}x-\frac{1}{2}y=0,\]
Ou encore : \[ (\text{AB})\;:\; \sqrt{3}x-y=0.\]
De plus, on a : \[ \vec{\text{BC}}\left(\begin{array}{c}\frac{1}{2}\\-\frac{\sqrt{3}}{2}\end{array} \right) ,\]
d’où : \[ (\text{BC})\;:\; -\sqrt{3}x-y+y_0=0.\]
\[\text{C}\in(\text{BC}) \Rightarrow y_0=\sqrt{3},\]
donc : \[ (\text{BC})\;:\; -\sqrt{3}x-y+\sqrt{3}=0.\]
Posons alors \(M(\alpha~;\beta)\) dans ce repère. On sait que la distance du point M à une droite (d) d’équation ax+by+c=0 est : \[ \text{d}(\text{M};(d))=\frac{\vert a\alpha + b\beta + c\vert}{\sqrt{a^2+b^2}}.\]
D’où : \[ \text{d}(\text{M};(\text{AB}))=\frac{\vert \alpha\sqrt{3} – \beta \vert}{\sqrt{\sqrt{3}^2+(-1)^2}}=\frac{\vert \alpha\sqrt{3}-\beta\vert}{2} \] et \[ \text{d}(\text{M};(\text{BC}))=\frac{\vert -\alpha\sqrt{3} – \beta+\sqrt{3} \vert}{\sqrt{(-\sqrt{3}^2+(-1)^2}}=\frac{\vert -\alpha\sqrt{3} – \beta+\sqrt{3}\vert}{2}. \]
De plus, \[ \text{d}(\text{M};(\text{AC}))=\beta.\]
De plus, M est toujours au-dessous de (AB), d’équation réduite : \[ y=x\sqrt{3}.\]
Donc : \[ \beta \leq\alpha\sqrt{3},\]
ce qui signifie que : \[ \alpha\sqrt{3}-\beta\geq 0\]
et donc : \[ \text{d}(\text{M};(\text{AB}))=\frac{\alpha\sqrt{3}-\beta}{2}. \]
De même, M est toujours au-dessous de (BC), d’équation réduite : \[ y=-x\sqrt{3}+\sqrt{3},\]
d’où : \[ \beta\leq-\alpha\sqrt{3}+\sqrt{3},\]
ce qui signifie que : \[ -\alpha\sqrt{3}-\beta+\sqrt{3}\geq 0\]
et donc :
\[ \text{d}(\text{M};(\text{BC}))=\frac{-\alpha\sqrt{3} – \beta+\sqrt{3}}{2}. \]
Ainsi,
\[ \text{d}(\text{M};(\text{BC})) + \text{d}(\text{M};(\text{AC})) + \text{d}(\text{M};(\text{AB}))=\frac{\alpha\sqrt{3}-\beta-\alpha\sqrt{3}-\beta+\sqrt{3}}{2}+\beta,\]
soit :
\[ \text{d}(\text{M};(\text{BC})) + \text{d}(\text{M};(\text{AC})) + \text{d}(\text{M};(\text{AB}))=\frac{\sqrt{3}}{2}.\]
La somme des 3 distances ne dépend donc pas de la position du point M.
Voir les fichiers sources \(\LaTeX\) du document PDF: