Volume d’une sphère avec une intégrale. Ceci est une sphère:

Si l’on considère que son rayon est égal à R alors son volume est \(\frac{4}{3}\pi R^3\)… mais pourquoi ?

Plaçons-nous dans un repère orthonormé de l’espace et plaçons-y notre sphère de sorte que son centre coïncide avec l’origine du repère :

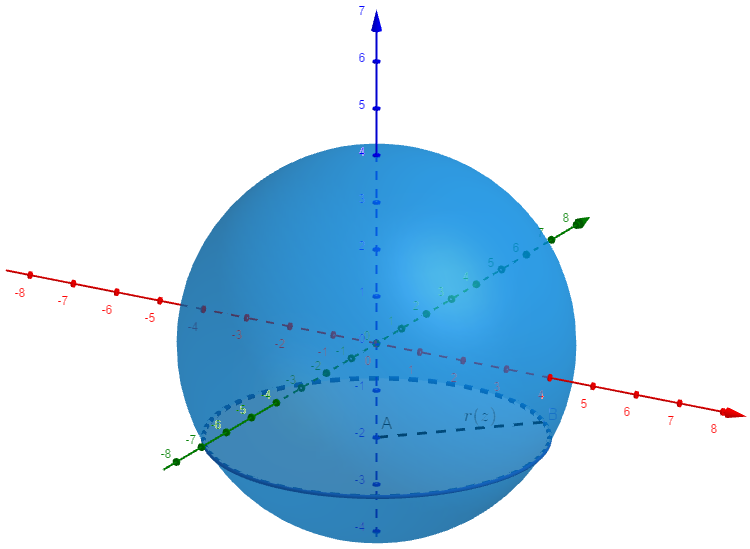
Nous avons aussi introduit un point A de coordonnées (0;0;z), où z varie de –R à +R. Nous avons ensuite considéré le disque de centre A et de rayon r(z), section de la sphère et du plan passant par A et parallèle au plan (xOy).

Le volume de la sphère n’est autre que la somme des aires des disques pour z variant de –R à +R, somme infinitésimale donc que l’on peut prendre comme une intégrale:$$\mathcal{V}=\int_{-R}^{+R}\pi r(z)^2\text{d}z.$$

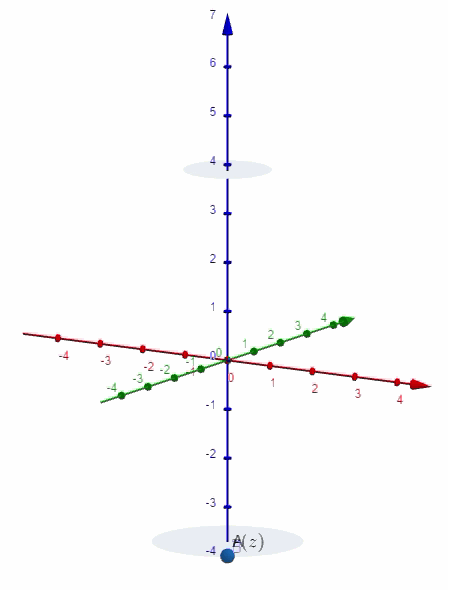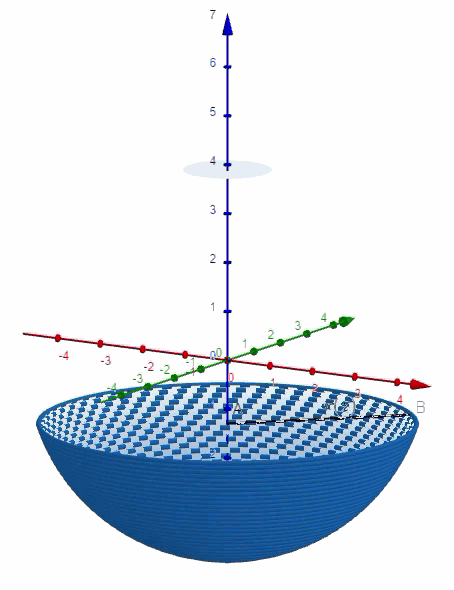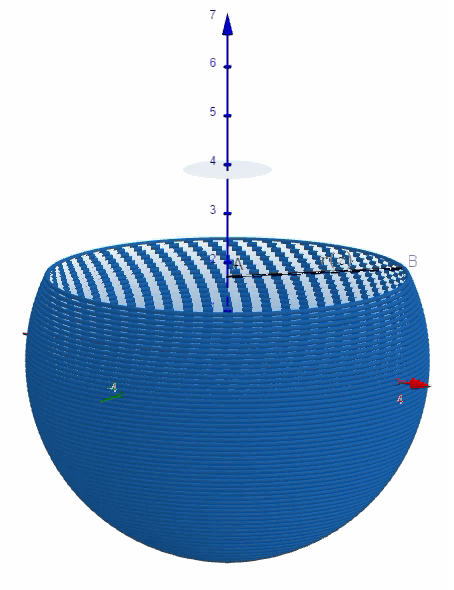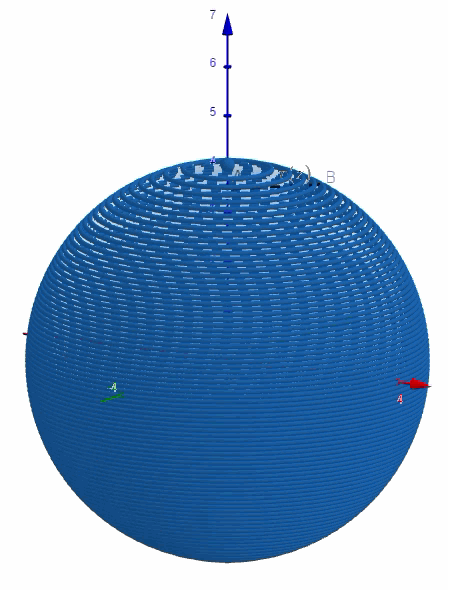
Il ne reste plus qu’à trouver l’expression de r(z)… et ce n’est pas trop compliqué car d’après le théorème de Pythagore, dans le triangle AOB:$$OB^2=OA^2+AB^2$$soit:$$R^2=z^2+\big[r(z)\big]^2$$d’où:$$r(z)^2=R^2-z^2.$$

Ça, c’est fait ! Il faut maintenant se pencher sur le calcul de l’intégrale:$$\begin{align}\mathcal{V}&=\pi\int_{-R}^{+R}(R^2-z^2)\text{d}z\\&=\pi\left[R^2z – \frac{1}{3}z^3\right]_{-R}^{+R}\\&=\pi\left[\left(R^3-\frac{1}{3}R^3\right) – \left(-R^3+\frac{1}{3}R^3\right)\right]\\&= \frac{4}{3}\pi R^3.\end{align}$$

On obtient alors la formule connue des collégiens ! Mystère résolu !