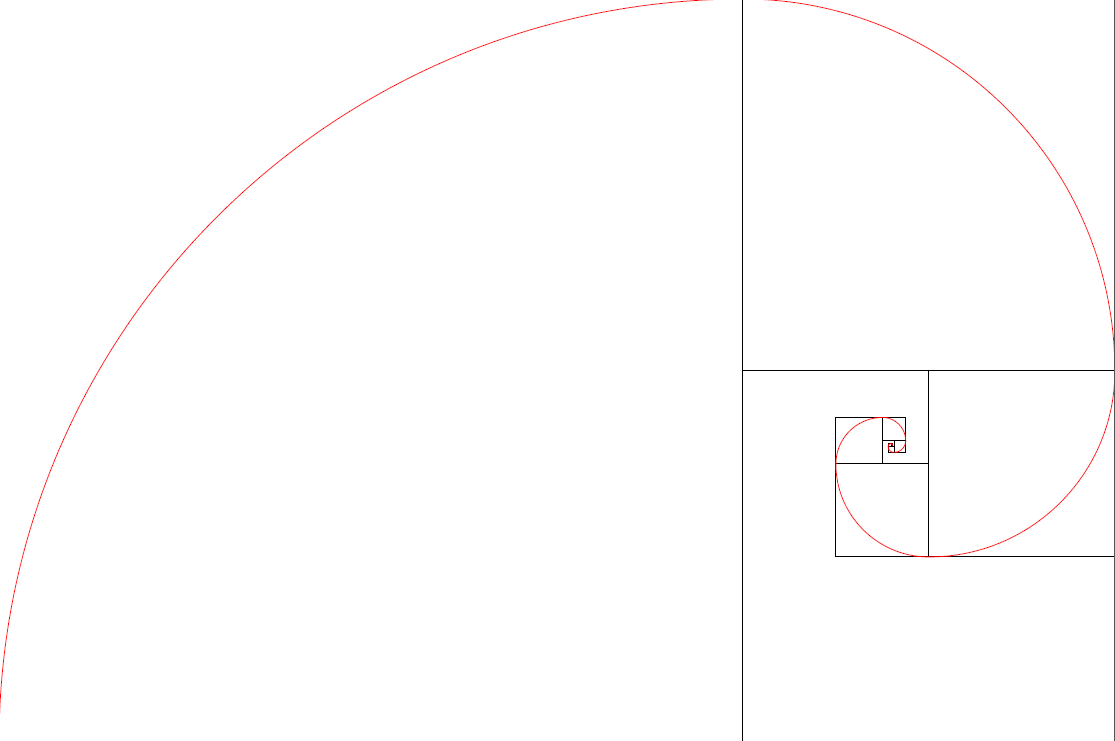
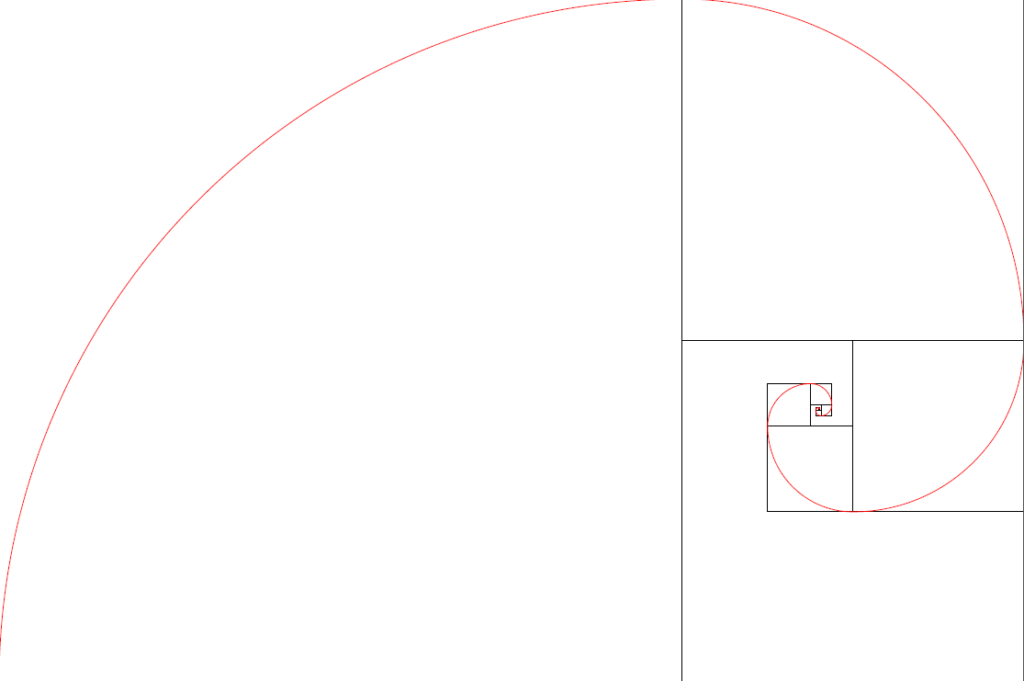
PythonTeX est une package réunissant \(\LaTeX\) et Python. Qui n’a jamais rêvé de compiler un programme Python pendant qu’il (elle) compilait son document \(\LaTeX\) ? Grâce à ce package, c’est possible ! Installation de PythonTeX Bien entendu, il faut au préalable installer Python sur votre ordinateur. Ensuite, vous devez installer le package […]
J’ai conçu des jeux de réflexion en Python: vous les trouverez ci-dessous. Le Memory’Pix Game Ce jeu permet de tester et de développer sa mémoire à court terme. Sudoku Ce jeu construit une grille de Sudoku et sa solution, et permet une exportation au format image et PDF (via \(\LaTeX\)). Les […]
Mes packages personnels LaTeX ont été écrits au fil du temps par la nécessité de posséder des outils qui n’existaient pas encore.
Certains sont proposés sur CTAN, d’autres non. Pour ceux qui ne figurent pas dans le catalogue officiel, il vous faudra les installer manuellement dans un répertoire déclaré dans votre distribution
(suite…)
tikz-tabular.sty est le nouveau package LaTeX que je viens de créé. Mais est-il réellement utile?
Je me pose cette question car après m’être pris la tête pour l’écrire, je trouve qu’il est un peu compliqué à l’utilisation… À vous de me le dire…
(suite…)
Construire un tableau de valeurs en Python est chose aisée à l’aide d’une boucle « for »… Aisé ? Réellement ? Obtenir les images de plusieurs valeurs l’est, mais construire un beau tableau l’est-il ? Je ne vais pas vous parler de LaTeX car je suis conscient que tout le monde ne passe pas par ce langage de programmation. Je vais rester en Python pur.
(suite…)
Faire un triangle de Pascal coloré en Python est un bon moyen de s’occuper alors que les vacances sont là. Je vais vous présenter plusieurs designs, mon préféré allant au dernier.
(suite…)
La fonction ifactors (que l’on peut trouver dans Xcas par exemple) peut être implémentée en Python.
Elle permet d’obtenir la liste des diviseurs d’un nombre ainsi que leur exposant dans la décomposition ne produit de facteurs premiers.
J’ai déjà traité le sujet de la décomposition en produits de facteurs premiers dans cet article (parlant de pythontex) et dans celui-ci (parlant de \(\LaTeX\)). Mais j’avais envie de me pencher sur la question algorithmique…
(suite…)
Manim est un module Python pour faire des animations « simplement ». Tout est relatif… Il m’a fallu quand-même quelques heures pour comprendre la logique du bousin. Mais au final, on peut faire des choses bien sympathiques… comme par exemple cette animation:
Nous allons aborder ici la notion de trinôme du second degré en Python sous un angle POO (Programmation Orientée Objet). J’avais en effet envie de construire une classe Python représentant un tel trinôme et pouvant effectuer toutes les opérations classiques du lycée.
(suite…)
Spirale et carrés, TiKZ et Python : il y a peu de temps, j’ai eu à construire une spirale inscrite dans une suite de carrés, avec TiKZ et à l’aide de Python :
Ceci était pour illustrer la somme des termes d’une suite géométrique.
(suite…)